Шпаргалка: Шпаргалка по Статистике

- вариационные (количественные) - строятся на основе количественного

группировочного признака.

При этом вариационные ряды по способу построения бывают:

· дискретными (прерывными) - ряд, который основан на прерывной вариации признака, т.е. в котором значение признака выражено целым числом (тарифный разряд рабочих, число раскрытых преступлений и т.д.).

· интервальными (непрерывными) - ряд, базирующийся на непрерывно изменяющемся значении признака, имеющего любые (в том числе и дробные) количественные выражения, т.е. значение признаков таких рядах задается в виде интервала.

Вариационные ряды состоят из двух элементов: вариант и частот.

Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота - это численность отдельных вариант или каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями. Сумма частот составляет объем ряда распределения.

5. Абсолютные показатели и их виды.

Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Абсолютные показатели могут быть только именованными числами, где единица измерения выражается в конкретных цифрах.

Абсолютные показатели следует также подразделить на:

· моментные - характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени.

· Интервальные - характеризуют итоговый объем явления за тот или иной период времени (например, выпуск продукции за квартал или за год и т. д.), допуская при этом последующее суммирование.

6. Относительные показатели: формы представления, виды.

7. Средняя арифметическая,способы ее расчета. Средняя гармоническая.

А) Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная имеет следующий вид:

где f - количество величин с одинаковым значением X (частота).

Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X остутствует нижнияя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.

Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин.

Б) Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

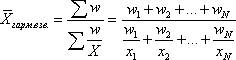
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

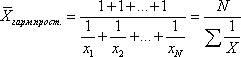
Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно - со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w1=w2 (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.

8. Средняя геометрическая и средняя хронологическая.