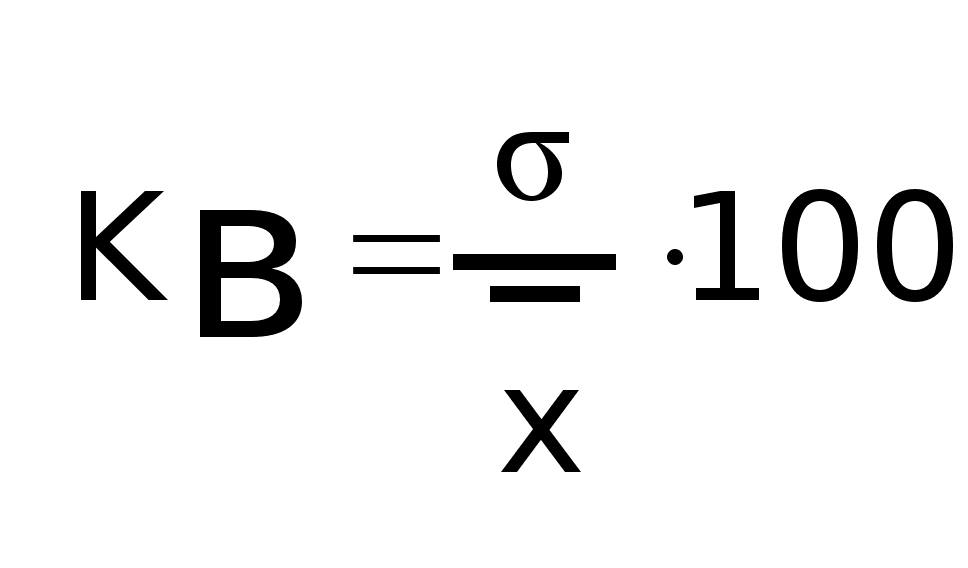Шпаргалка: Статистика (шпаргалка 2002г.)

Σf_Оf-1; Σf_О2-1 - суммы частот всех интервалов, предшествующих

децильным;

f_D1; f_D3 - частоты децильных интервалов

3.5. Понятие вариации признака, показатели вариации, дисперсия альтернативного признака. Упрощенный способ расчета дисперсии. Виды дисперсий в совокупности, разбитой на группы, правило сложения дисперсий

Способность признака принимать различные значения называют вариацией признака. Для измерения вариации признака используют различные обобщающие показатели – абсолютные и относительные.

1. Размах вариации – это разность максимального и минимального значений признака: R = х_max - х_min.

2. Среднее линейное отклонение – это средняя из абсолютных значений отклонений признака от своей средней:

3. Средняя из квадратов отклонений значений признака от своей средней, т.е. дисперсия:

Дисперсия есть разность среднего квадрата и квадрата средней

или - простая

- взвешенная

Дисперсия может быть определена методом условных моментов. Момент распределения – это средняя m отклонений значений признака от какой-либо величины А: если А = 0, то момент называется начальным; если А = , то моменты – центральными; если А = С, то моменты – условными.

В зависимости от показателя степени К, в которую возведены отклонения (х – А)^к, моменты называются моментами 1-го, 2-го и т.д. порядков.

Расчет дисперсии методом условных моментов состоит в следующем:

1. Выбор условного нуля С;

2. Преобразование фактических значений признака х в упрощенные хґ путем отсчета от условного нуля С и уменьшения в d раз:

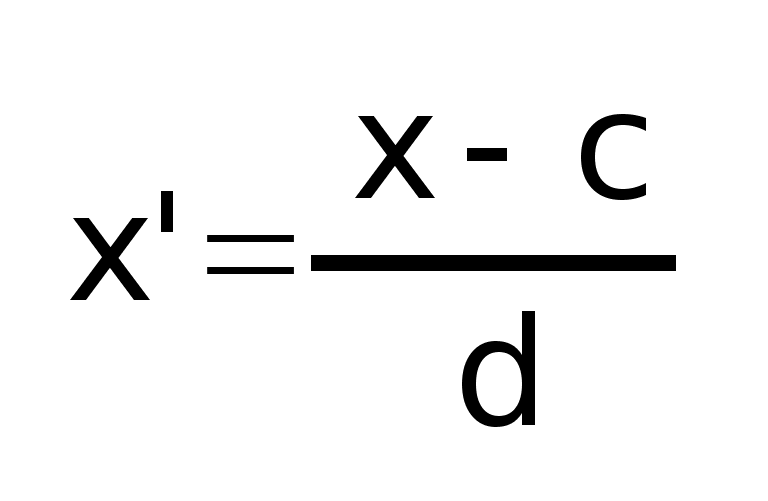
3. Расчет 1-го условного момента:

4. Расчет 2-го условного момента:

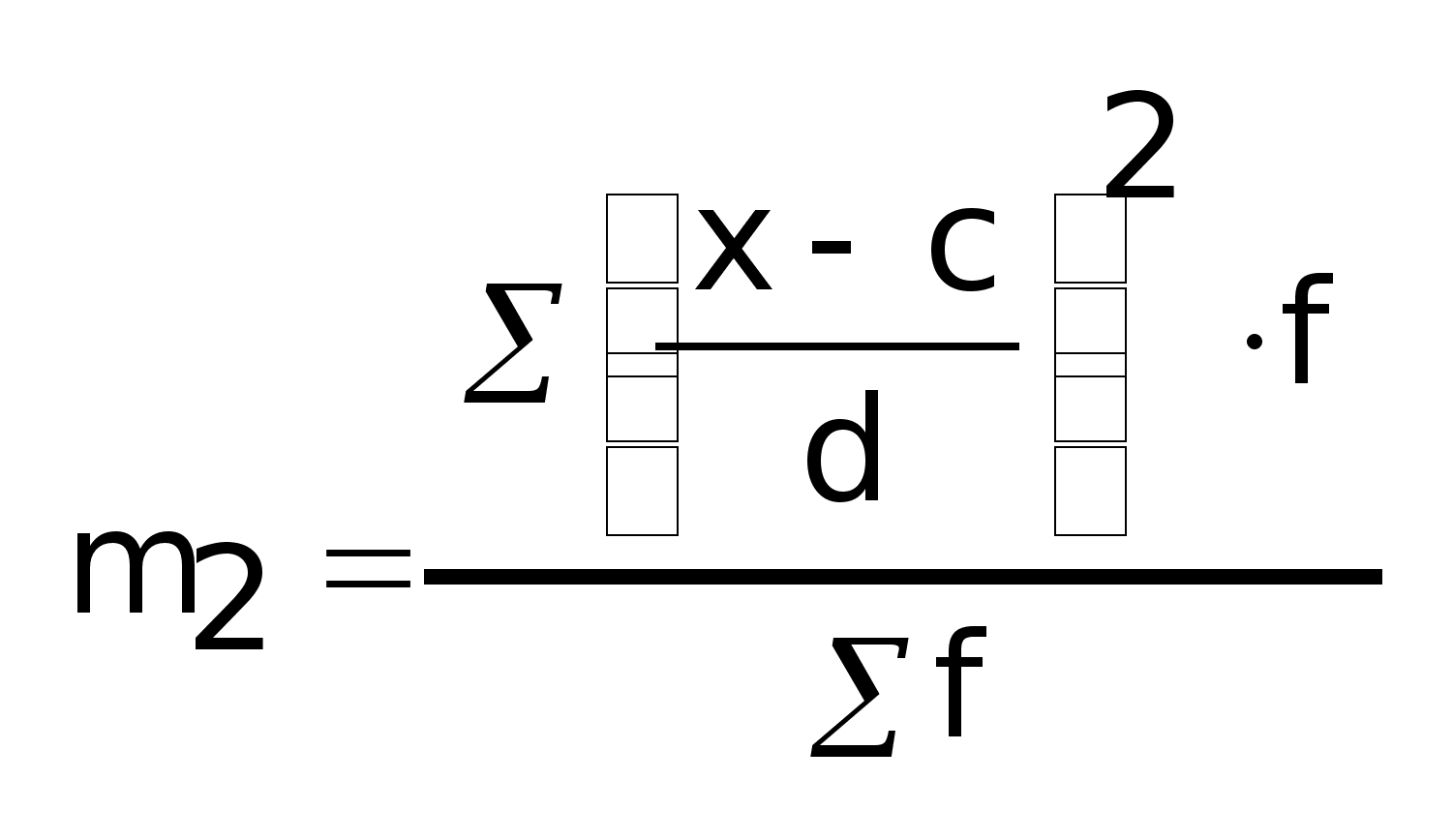
5. Расчет 1-го порядка начального момента:

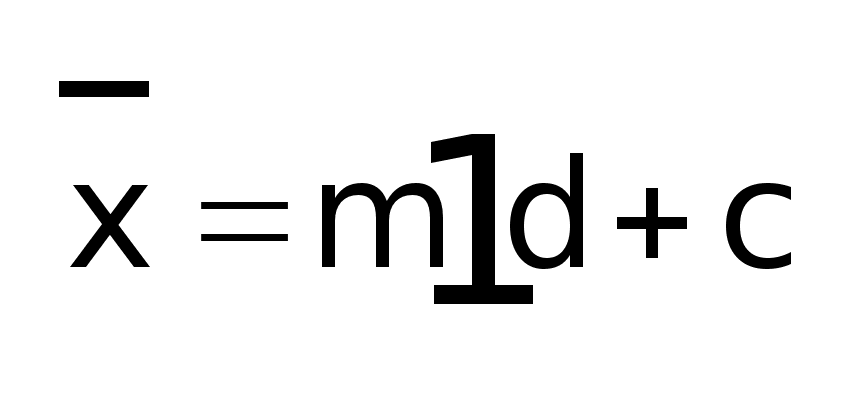
6. Дисперсии

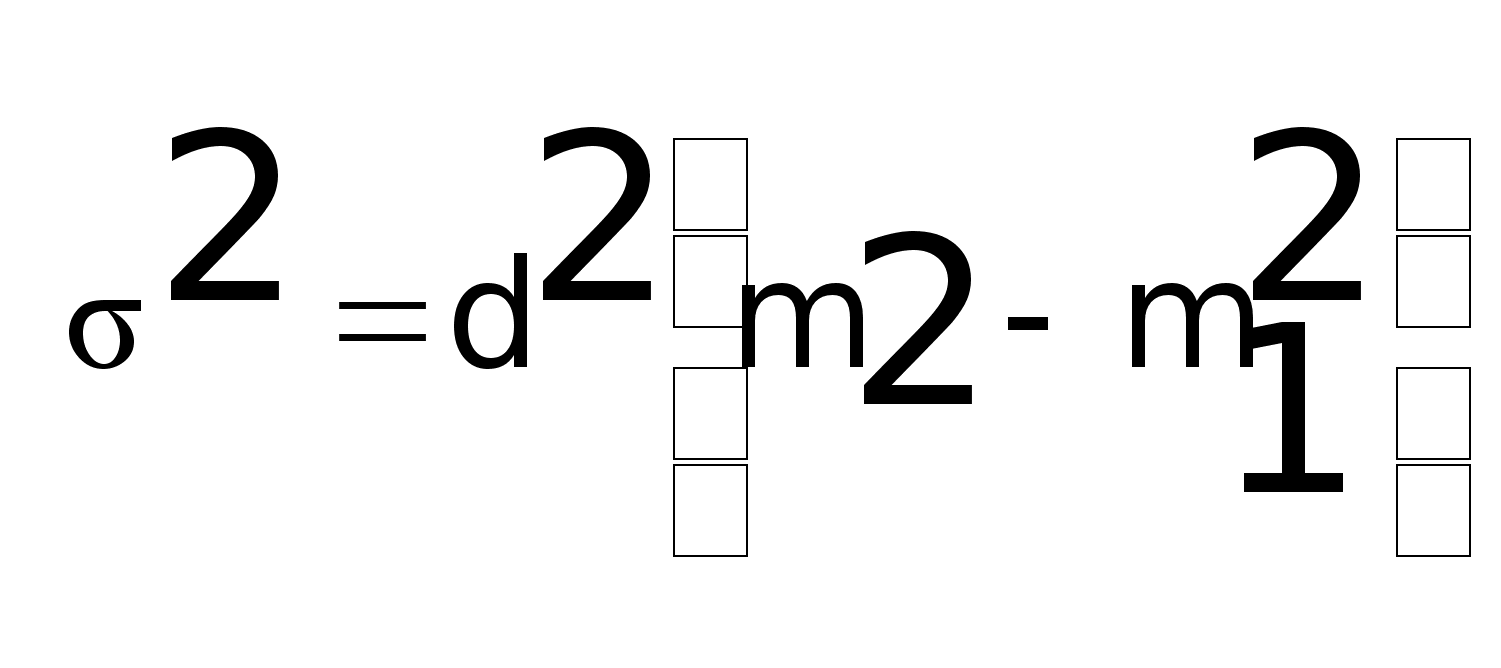
Среднее квадратичное отклонение рассчитывается по данным о дисперсии  = ²

Относительные величины вариации

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней

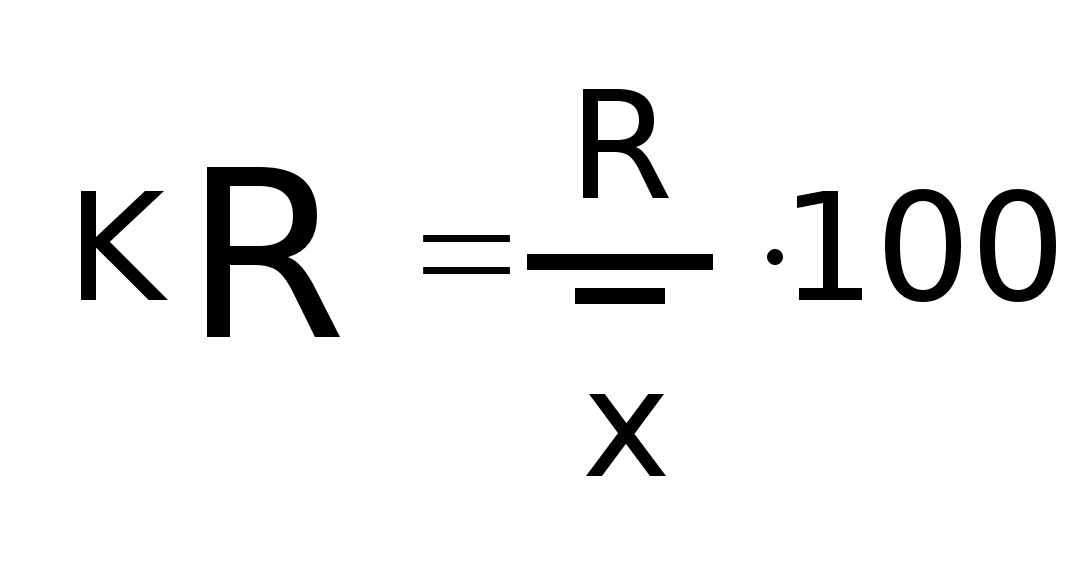
2. Относительное линейное отклонение:

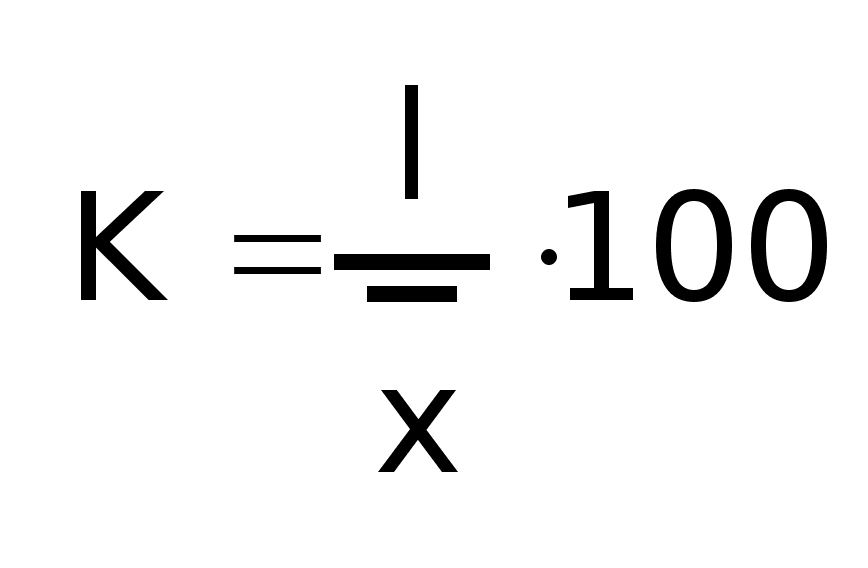
3. Коэффициент вариации: