Статья: Алгебраические кривые и диофантовы уравнения
Те, кому посчастливилось ходить на уроки математики ещё до введения теории множеств в школьную программу, несомненно, помнят теорему Пифагора, :
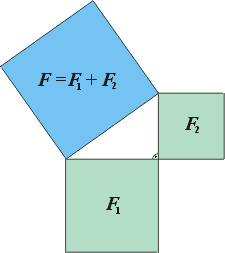
В прямоугольном треугольнике сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе (рис.1).
Эта теорема была известна в Вавилонии уже во времена Хаммурапи, а возможно, её знали и в древнем Египте, однако впервые она была доказана, по-видимому, в пифагорейской школе. Так называлась группа интересующихся математикой философов по имени основателя школы Пифагора (ок. 580–500 г. до н. э.) – личности довольно мифической. Это был мистик, учёный и политик аристократического толка. Он, должно быть, путешествовал по Вавилонии и Египту, а позднее на юге Италии, в Кротоне, собрал вокруг себя кружок увлечённых юношей, из которого и возникла пифагорейская школа. В настоящее время уже невозможно установить, какие достижения пифагорейцев принадлежат самому учителю, а какие следует приписать его ученикам.
Рис.1 |
Рис.2 |
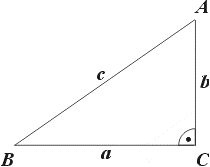
Пусть длины сторон прямоугольного треугольника ABC (рис.2) обозначены через a, b, c, причём сторона длины c находится напротив прямого угла. Теорема Пифагора утверждает справедливость равенства
| (1) | a2 + b2 = c2 . |
Оно выполняется, например, если вместо a, b, c подставить числа 3, 4, 5, или 5, 12, 13, или 41, 140, 149. Такие решения уравнения (1) в целых положительных числах нашли уже пифагорейцы, и потому такие решения называют пифагоровыми тройками. Вполне возможно, что поиски этих троек и привели к теореме Пифагора. Впрочем, тройка (3, 4, 5) была известна значительно раньше, о чём свидетельствует, скажем, дошедший до нас диалог императора Чжоу-гуна (ок. 1100 г. до н. э.) и учёного Шан Гао ([2 ], стр. 54–65); более подробно о тройке (3, 4, 5) рассказывается в предыдущей лекции Ю. Рольфса.
Зададимся вопросом, сколько существует пифагоровых троек. Очевидно, умножая все три числа на любое целое n, можно из тройки (a, b, c) получить бесконечно много новых троек; из тройки (3, 4, 5) возникает таким образом последовательность троек (3, 4, 5) (6, 8, 10), (9, 12, 15), (12, 16, 20), ... . Поэтому уточним поставленный вопрос и будем искать простейшие пифагоровы тройки (a, b, c), т.е. те, у которых наибольший общий делитель чисел a, b и c равен 1. Решение этой задачи указал ещё Диофант из Александрии (ок. 250 г. н. э.):
| Если n и m – два взаимно простых целых (положительных) числа, разность которых n – m положительна и нечётна, то (2nm, n2 – m2 , n2 + m2 ) – простейшая пифагорова тройка, и любая из таких троек может быть найдена этим способом. |
Первая часть утверждения легко проверяется непосредственной подстановкой; частные случаи этого «правила построения» пифагоровых троек были известны и раньше. Более сложно доказать, что таким образом получаются все простейшие тройки. Сейчас мы установим это с помощью геометрических соображений. Разделив равенство (1) на c², получим
| ( |
a c | ) | 2 | + | ( |
b c | ) | 2 | = 1. |
Поэтому каждая пифагорова тройка (a, b, c) дает решение уравнения
| (2) | x2 + y2 = 1 |
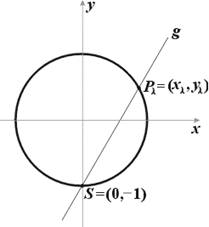
Рис.3
в рациональных числах (дробях), а именно x = a/c, y = b/c; назовём такую пару рациональным решением уравнения (2). Наоборот, из всякого такого решения, если привести дроби x и y к общему знаменателю: x = a/c, y = b/c, где a, b, c – целые, тотчас возникает пифагорова тройка. Следовательно, наша задача сведена к определению рациональных решений уравнения (2). Это уравнение также хорошо известно из школы – оно задаёт на евклидовой плоскости окружность с центром в начале координат и радиусом 1 (рис.3). Если рассмотреть прямую g с угловым коэффициентом l, проходящую через точку (0, –1):
| (3) | g: y = lx – 1, |
то координаты обеих точек пересечения S = (0, –1) и Pl = (xl , yl ) прямой g с окружностью удовлетворяют уравнениям (2) и (3). Подставляя (3) в (2), получаем
| (4) | (l2 + 1) x2 – 2lx = 0, |
откуда можно найти координаты (xl , yl ) точки Pl :
| (5) |
|
(Легко убедиться подстановкой, что они являются решением уравнения (2).) При рациональных l эти решения, очевидно, будут рациональными. Обратно, если (x0 , y0 ) – рациональное решение уравнения (2) и P0 – соответствующая ему точка на окружности, то угловой коэффициент прямой, проходящей через точки (0, –1) и P0 , рационален: l = (y0 + 1)/x0 . Следовательно, (x0 , y0 ) есть решение вида (5). Таким образом, доказано, что все рациональные решения уравнения (2) находятся по формулам (5) с рациональным l. Если записать l в виде дроби: l = n/m, то формулы (5) перепишутся так:
| xl = | 2nm n2 + m2 | , yl = | n2 – m2 n2 + m2 | . |
Итак, любая пифагорова тройка представима в виде (2nm, n2 – m2 , n2 + m2 ), что и требовалось доказать.
Приведённый результат – лишь один из многих, содержащихся в «Арифметике» Диофанта. До нашего времени сохранились 6 книг этого сочинения; об их общем числе можно только строить догадки. Неизвестно также, кем был Диофант. Во всяком случае, его труд – одно из самых великолепных сочинений античной эпохи, в котором собраны весьма разнообразные задачи и часто с чрезвычайно остроумными решениями. (Более подробные сведения интересующийся читатель может найти в удачной книжечке Башмаковой [1 ].)
Именно сочинение Диофанта – изданное в 1621 г. в переводе Клода Гаспара де Баше де Мезирьяка (1581–1630) – дало повод Пьеру Ферма записать на полях перевода одно из самых достопримечательных и далеко поведших замечаний в истории математики:
|
«Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.» «Невозможно разложить куб на два куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две степени с тем же самым показателем; я нашёл этому поистине чудесное доказательство, однако поля слишком малы, чтобы оно здесь уместилось». |
Таким образом, большая теорема Ферма утверждает, что уравнение
| (6) | an + bn = cn |
ни при каком натуральном n, большем 2, неразрешимо в целых положительных числах.
Общее доказательство сформулированного утверждения не удалось найти до сих пор, несмотря на то что этим занимались поколения математиков. [Напомню, что лекции эти были читаны в 70-е годы, а Эндрю Уайлз и Ричард Тейлор опубликовали доказательство теоремы Ферма в 1995 г. Любой поисковик (search engine) выдаст кучу ссылок в Интернете на эту тему, я же приведу только одну публикацию – D.Goldfeld. "Beyond the Last Theorem", опубликованную в журнале "The Sciences". – E.G.A.] Вероятнее всего, Ферма ошибался, предполагая, что располагает решением. В 1908 г. Пауль Вольфскель завещал премию в сто тысяч марок тому, кто первым представит доказательство. В результате инфляции после первой мировой войны величина премии в настоящее время составляет едва десятую часть первоначальной суммы (см. [15 ], лекция 1, пункт 7). К тому же, как указывает Г. Эдвардс в своей книге [5 ] о теореме Ферма, премия назначена лишь за доказательство предположения – контрпример не принесёт ни пфеннига!
Справедливость большой теоремы Ферма для некоторых частных случаев была установлена уже довольно давно: сам Ферма доказал неразрешимость уравнения (6) при n = 4, Л. Эйлер – при n = 3 (1770 г.), А. Лежандр – при n = 5 (1825 г.) и Г. Ламе – при n = 7 (1839 г.). Самые замечательные результаты здесь принадлежат, однако, Э. Куммеру (1810–1893), который своими исследованиями по проблеме Ферма оказал решающее влияние на развитие алгебраической теории чисел. В нашем столетии его методы были усовершенствованы и дополнены (1929 г. и позже) прежде всего благодаря усилиям У. Вандивера, Д. Лемера и Э. Лемера, так что к настоящему времени неразрешимость уравнения (6) доказана (с использованием ЭВМ) для всех n £ 125000 (З. Вагштафф, 1976 г.; см. также [15 ], лекция 2, «Последние результаты»). Если принять во внимание, что число 2125000 записывается посредством 37628 цифр, то поиски контрпримера к большой теореме Ферма представляются совершенно безнадёжным занятием!
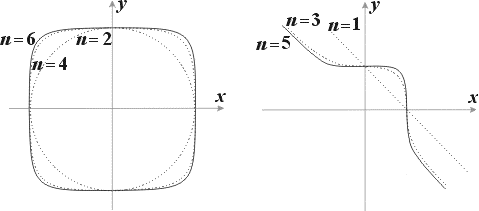
Рис.4
Рассуждения, аналогичные проведённым при нахождении пифагоровых троек, показывают, что проблема Ферма сводится к определению рациональных решений уравнения
| (7) | xn + yn = 1. |
Рассмотрев на евклидовой плоскости кривую Fn , заданную этим уравнением, получим две качественно различные возможности в зависимости от чётности или нечётности n (см. рис.4). Кривая Fn называется кривой Ферма порядка n. Поэтому гипотеза Ферма означает, что на кривой Fn порядка выше 2 единственными рациональными точками (т.е. точками с рациональными координатами) являются точки пересечения с осями координат.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--