Статья: Алгебраические кривые и диофантовы уравнения
Порядок кривой C, т.е. максимальная из степеней i + j одночленов xi yj , входящих в уравнение (8), служит грубой мерой сложности кривой. Очевидно, что чем выше порядок, тем труднее найти рациональные решения уравнения (8). Это обстоятельство находит более точное выражение в гипотезе Морделла:
| На кривой, порядок которой выше или равен четырём, имеется лишь конечное число рациональных точек. |
Здесь следует сделать оговорку, что рассматриваются кривые «общего вида» 1 , а вырожденные случаи во внимание не принимаются.
Относительно справедливости гипотезы Морделла известно очень мало; единственным общим результатом здесь является теорема Зигеля ([16 ], 1929 г.):
| На кривой общего вида, порядок которой выше 2, лежит лишь конечное число целых точек (точек с целыми координатами), т.е. у соответствующего уравнения (8) существует лишь конечное число целочисленных решений. |
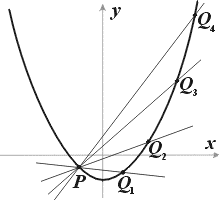
Для кривых малого порядка d картина следующая: при d = 1 имеем прямую и на ней бесконечно много рациональных (и даже целых) точек; при d = 2 получается квадрика (эллипс, парабола, гипербола); на квадрике либо совсем нет, либо бесконечно много рациональных точек 2 . Это доказывается тем же геометрическим методом, который выше был применён для нахождения рациональных точек на единичной окружности и который, согласно данным Башмаковой, также восходит к Диофанту ([1 ], § 5). И именно, прямая с рациональным угловым коэффициентом, проходящая через рациональную точку P квадрики, пересекает её в рациональных точках. Поворачивая прямую вокруг точки P, получаем бесконечно много рациональных точек (рис.5).
Рис.5 |
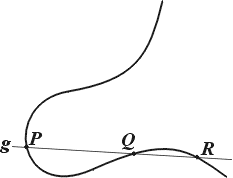
Рис.6 |
Случай d = 3 является в известном смысле промежуточным между рассмотренными. Как мы видели, на кривой Ферма F3 (рис.4) лежат лишь две рациональные точки, а сейчас мы приведём пример кривой третьего порядка, на которой бесконечное число рациональных точек. Для этого воспользуемся следующим методом секущих, представляющим собой обобщение указанного ранее способа для квадрик (и этот метод тоже встречается у Диофанта; см. [1 ], § 6):
| Если P и Q – две рациональные точки кривой C третьего порядка и прямая, проходящая через P и Q, пересекает кривую C ещё в одной точке R, то R также является рациональной точкой (рис.6). |
Это утверждение доказывается очень просто. Если
| (9) | g: y = rx + s |
– уравнение прямой, проходящей через точки P и Q, то r и s – рациональные числа, ибо их можно выразить через координаты (xP , yP ) и (xQ , yQ ) точек P и Q по формулам
| r = | yP – yQ xP – xQ | , s = yP – r xP = | xP yQ – yP xQ xP – xQ | . |
Подставив (9) в уравнение кривой C, получим для x уравнение третьей степени
| (10) | x3 + ax2 + bx + c = 0 |
с рациональными коэффициентами a, b, c. По условию корнями его являются абсциссы точек пересечения P, Q и R прямой g с кривой C, т.е. xP , xQ , xR . Однако, зная корни уравнения, можно найти его коэффициенты совершенно так же, как это делается в школе для квадратного уравнения. Например, сумма корней, взятая с противоположным знаком, равна коэффициенту при x2 :
| xP + xQ + xR = –a. |
По предположению xP и xQ рациональны, поэтому рациональным будет и xR , а значит, и yR = r xR + s, т.е. R – рациональная точка, что и требовалось доказать.
Опробуем этот способ на кривой E, заданной уравнением
| (11) | E: y2 = x3 – 25x, |
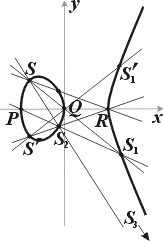
Рис. 7.
отправляясь от точек P = (–5, 0), Q = (0, 0), R = (5, 0) и S = (–4, 6) (рис.7). Сначала, используя прямую SQ получим точку S1 с координатами (61 /4, –93 /8), затем получим точку S2 = (5 /9, –319 /27), далее точку S3 = (12473 /961, –4013790 /29791) и т.д. Из уравнения (11) видно также, что кривая E симметрична относительно оси х: вместе с каждой точкой T(xT , yT ) на кривой лежит и симметричная ей относительно оси x точка T'(xT , –yT ), и если точка T рациональна, то и T' будет рациональной. Это можно подогнать под описанный выше метод секущих следующим образом: дополним кривую E «несобственной точкой» O в направлении оси y. Прямые, проходящие через O, – это прямые, параллельные оси y, и мы можем получить точку T' как «третью точку пересечения» прямой, проходящей через O и T, с кривой E. Далее, можно использовать предельный случай метода секущих – метод касательных: вместо прямой, проходящей через рациональные точки P и Q, брать касательную t к кривой в рациональной точке P (считая точки P и Q совпавшими). Рассуждениями, аналогичными проведённым ранее, можно показать, что точка пересечения прямой t с кривой E тоже будет рациональной (и опять это было известно уже Диофанту; см. [1 ], § 6).
В разобранном выше примере создается – и совершенно справедливо – впечатление, что проводимые построения никогда не заканчиваются и позволяют найти бесконечно много рациональных точек на кривой E. Затруднения могли бы возникнуть, лишь если бы мы после конечного числа шагов вернулись к одной из ранее полученных точек, но это представляется весьма маловероятным ввиду всё усложняющихся знаменателей.
Следующее утверждение было высказано в 1901 г. А. Пуанкаре (1854–1912) [14 ], а доказано только спустя 20 лет (в 1922 г.) Л. Морделлом [9 ]:
| Все рациональные точки кривой третьего порядка можно получить из некоторого конечного их числа с помощью описанного способа построения. |
Как и в теореме Зигеля, кривая считается «пополненной» своими несобственными точками, и кроме того, предполагается, что она является кривой общего вида (т.е. не имеет особенностей). Такие кривые называются эллиптическими 3 .
Сформулированная выше теорема Морделла была обобщена в двух различных направлениях: вместо рациональных точек стали рассматривать точки с координатами из заданного числового поля, а вместо эллиптических кривых – поверхности произвольной размерности (так называемые абелевы многообразия). Начало этим обобщениям было положено А. Вейлем, и окончательный результат называют сейчас теоремой Морделла–Вейля.
В связи с этими вопросами о рациональных точках за последние 15 лет появился ряд отчасти фантастических гипотез (Б. Бёрч, X. П. Суиннертон-Дайер, Дж. Тэйт, Э. Огг; см. обзорную статью [17 ]). Справедливость некоторых из них недавно была подтверждена в проложившей новые пути работе Б. Мазура ([8 ], 1976 г.). Речь идёт о вопросах, связанных с так называемой «тонкой структурой» рациональных точек на эллиптической кривой, и об этом мне хотелось бы немного рассказать в заключение.
Рассмотрим эллиптическую кривую E, заданную в канонической форме Вейерштрасса, т.е. уравнением вида
| (12) | E: y2 = x3 + ax2 + bx + c |
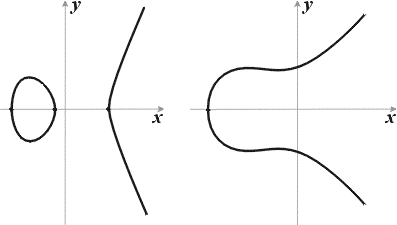
Рис.8
с целочисленными коэффициентами a, b и c. Качественно возможны два показанных на рис.8 случая, в соответствии с тем, один или три вещественных корня имеет многочлен в правой части (12) (эти корни соответствуют точкам пересечения E с осью x). Будем опять считать кривую E пополненной несобственной точкой O в направлении оси y. Следуя А. Пуанкаре [14 ], определим на кривой E операцию P*Q: для любых точек P и Q точка P*Q – это третья точка пересечения прямой PQ с кривой E, симметрично отражённая относительно оси х (рис.9).
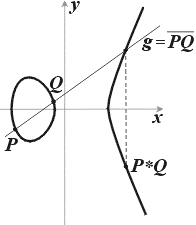
Рис. 9.
Легко видеть, что введённая операция коммутативна (т.е. P*Q = Q*P), что точка O является для неё нейтральным элементом (т.е. O*P = P*O) и что для каждой точки P существует обратный элемент – симметричная ей относительно оси x точка P' (т.е. P*P' = O = P'*P). Несколько сложнее доказать, что эта операция ассоциативна (т.е. (P*Q)*R = P*(Q*R) для любых точек P, Q, R). На языке современной математики это означает, что точки кривой E образуют коммутативную группу относительно операции *.
Из предыдущих рассуждений следует, что для любых двух рациональных точек P, Q точка P*Q также рациональна, – собственно, это и послужило исходным пунктом нашего метода секущих для построения рациональных точек. Итак, рациональные точки Erat кривой E образуют подгруппу группы E. (Несобственная точка O считается рациональной.)
Искушённый читатель легко заметит, что теорему Морделла можно теперь сформулировать так:
| Рациональные точки эллиптической кривой образуют конечно-порождённую коммутативную группу. |
Эта формулировка имеет определённые преимущества, так как для таких групп известны структурные теоремы. Например, группу Erat можно представить в виде произведения некоторой конечной группы TE и конечного числа бесконечных циклических групп. Количество бесконечных циклических сомножителей называется рангом эллиптической кривой E, а конечная группа TE – её группой кручения. О ранге известны до сих пор только отдельные факты. Так, А. Нерон ([11 ], 1953 г.) доказал, что существует кривая, ранг которой не меньше 10, не приведя, правда, явного примера. А. Виман ([20 ], 1948 г.) построил пример кривой ранга ³4, Д. Пенни и К. Померанс ([13 ], 1975 г.) дали пример кривой ранга ³7, а Ф. Грюневальд и Р. Циммерт ([6 ], 1977 г.) – кривой ранга ³8 4 ; к числу кривых ранга ³8 относится, например, кривая, задаваемая уравнением (12) с коэффициентами a = –32 ×1487×1873, b = 25 ×32 ×5×151×14551×33353, c = 28 ×34 ×52 ×7×1512 ×193×277×156307. Рассмотренная ранее кривая (11) (рис.7) имеет ранг 1, соответствующая бесконечная циклическая подгруппа порождается точкой S = (–4, 6). Это следует из результатов Р. Вахендорфа ([19 ], 1974 г.), который исследовал кривые, задаваемые уравнениями вида y2 = x3 – p2 x, где p – простое.
Пока неясно, существуют ли эллиптические кривые сколь угодно большого ранга (что считается весьма вероятным). Известно, однако, что ранг оценивается через коэффициенты уравнения (12) (точнее, через число различных простых сомножителей отдельных коэффициентов [18 ]). Поэтому неудивительно, что в построенных примерах кривых высокого ранга уравнения имеют большие коэффициенты. Согласно одной из упомянутых выше гипотез, ранг эллиптической кривой E равен кратности нуля так называемого L-ряда LE (z) кривой E в точке z = 1 (Бёрч и Суиннертон-Дайер [3 ]).
Рассмотрим, наконец, группу кручения TE . Она состоит из рациональных точек P конечного порядка (т.е. из тех, для которых n-кратная композиция P*P*...*P равна O при некотором n), называемых (рациональными) точками кручения. Прежде всего на основании самого вида кривой можно заключить, что справедлива следующая общая структурная теорема: группа TE либо сама циклична, либо есть произведение группы Z2 порядка 2 на циклическую группу. Это можно обосновать следующим образом. Кривая E (пополненная) состоит из одной или двух замкнутых линий (см. рис.8), а потому топологически выглядит как одна или две окружности. При этом часть E0 , содержащая (несобственную) точку O, образует подгруппу. Можно доказать, что любая конечная подгруппа в E0 циклическая (это делается точно так же, как для группы вращений окружности). Следовательно, если группа кручения TE целиком лежит в E0 , то TE – циклическая группа. В противном случае TE есть произведение Z2 на группу T0 E точек кручения из E0 .
О группе кручения кое-что было известно уже довольно давно. Так, Т. Нагелль ([10 ], 1935 г.) и, позднее, Л. Лутц ([7 ], 1937 г.) получили следующий интересный результат, дающий одновременно метод для явного определения точек кручения конкретных кривых:
|
Если Р – (рациональная) точка кручения эллиптической кривой Е, заданной уравнением y2 = x3 + ax2 + bx + c К-во Просмотров: 354
Бесплатно скачать Статья: Алгебраические кривые и диофантовы уравнения
|