Содержание

Введение

Глава 1. Классификация конфигураций решеток

Глава 2. Аутополиплоидизация генератора

Глава 3. Применение ГА и результаты

Заключение

Список литературы

Введение

Природа часто дает инженерам уникальную возможность понять суть методов, необходимых для решения сложных конструкторских задач. Конструирование, основанное на природных аналогиях, предоставляет инженерам множество уникальных и мощных средств проектирования. К примеру, генетические алгоритмы (ГА), относительно новый класс стохастических методов общей оптимизации, возникли из дарвиновских понятий о естественном отборе и эволюции. Аналогичным образом поведение роя насекомых или стаи птиц подсказало недавно идею оптимизации по принципу роения элементов (ОПРЭ). Нейронные сети (НС) и нечеткая логика (НЛ) созданы по принципу процесса принятия решения человеком. Фрактальная геометрия возникла из потребности наилучшим образом описать чрезвычайно неправильные формы естественных объектов, таких как береговая линия, топография местности, форма облаков, снежинок, растений, листьев, деревьев. Методы, заимствованные из природы, широко используются в последнее время, чтобы найти эффективные решения все более сложным задачам в области электромагнетизма.

Используется специально разработанный ГА, с помощью которого создаются оптимизированные равномерно-возбуждаемые решетки, базирующиеся на произвольных фрактальных геометриях и называемые полифрактальными решетками (ПФР). Как оказалось, такой метод имеет несколько важных преимуществ по сравнению с обычными подходами к оптимизации решеток. Во-первых, характерная фрактальная геометрия ПФР дает простой и компактный способ описания весьма сложных структур с помощью небольшого числа параметров. Именно это уникальное свойство и положили в основу эффективной схемы кодирования ГА, применяемой для оптимизации ПФР. Во-вторых, благодаря возможности итеративного получения целых сегментов ПФР, удалось создать быстрый алгоритм формирования ДН, необходимый для эффективного расчета связанных между собой ДН. Этот алгоритм значительно сокращает время оценки пригодности (соответствия) каждого элемента группы, что, в свою очередь, снижает общее время, требуемое для выполнения ГА. Фрактальная схема кодирования в сочетании с быстрым алгоритмом формирования ДН позволяет применять подход ГА для разработки гораздо бо льших оптимальных конфигураций решеток, чем было ранее возможно.

В данной статье мы развиваем идею, представленную ранее в [13-14], в направлении усовершенствования разработки ПФР за счет периодического применения хромосомо-подобного расширения, основанного на аутополиплоидии, которое позволяет - в ходе процесса оптимизации - увеличивать степень произвольности получаемых антенных решеток. Сутью проблемы создания антенной решетки является получение полностью произвольной конфигурации, поскольку она обладает наивысшей степенью свободы. Тогда положение любого антенного элемента в конструкции решетки было бы независимым параметром. Однако если иметь при расчете большое число параметров, оптимизационные процессы типа ГА часто становятся очень сложными. Более того, прямой расчет множителя для произвольных решеток может стать очень затратным, особенно для решеток большого размера (т.е. с большим N). В данной статье мы описываем процесс, при котором происходит удвоение числа генераторов (функций), используемых для описания ПФР. Этот процесс, называемый нами аутополиплоидизация генератора , заменяет каждый генератор двумя его копиями, идея чего заимствована из аутополиплоидизационной мутации, имеющей место в природе. По мнению биологов, такая мутация сильно повлияла на эволюцию растений и животных, обеспечив дополнительную степень свободы, что способствовало эволюционным процессам и в то же время сохраняло особенности, характерные для предыдущего поколения организмов. В используемом нами ГА мы моделируем аутополиплоидизацию путем удвоения генераторов фрактально-произвольной структуры и путем произвольного применения одной из его копий везде, где применялся исходный генератор. Такой метод создает в конце концов однородную структуру антенной решетки, удваивая при этом число параметров, используемых для ее описания. После этого появляется возможность разработки каждого генератора независимо от других, что дает искомую гибкость процесса разработки и обеспечивает бо льшую произвольность ПФР, чем ранее. Ступень разработки, называемая периодом, продолжается до тех пор, пока оптимизация не достигнет своего предела. Достигнув предела в рамках периода, мы выполняем аутополиплоидизацию генератора по каждому члену совокупности и далее начинаем следующий период разработки. Таким образом, этот цикл можно использовать для эффективной разработки оптимизированных произвольных решеток на базе периодических, детерминистских фрактальных или иных ранее детерминированных ПФР.

Глава 1. Классификация конфигураций решеток

Антенные решетки можно классифицировать по разным основаниям; в данной статье мы выбрали широкий класс конфигураций, объединяемых по признаку однородного возбуждения (намагничивания) элементов. Самыми распространенными здесь являются периодическая и произвольная решетки. Такие решетки являются полярно противоположными с точки зрения их геометрии и характеристик. Периодические решетки способны иметь относительно низкие уровни боковых лепестков, но являются не очень устойчивыми. Произвольные решетки, с другой стороны, устойчивы, но им обычно не присущ низкий уровень боковых лепестков. Поэтому периодические и произвольные решетки наилучшим образом пригодны только для своих специфических применений.

Помимо указанных конфигураций возможны и иные, основанные на ряде разнообразных подходов к расчету их геометрии. К примеру, оказалось, что весьма ценные особенности имеют конфигурации, построенные на фрактальных геометриях [19-21]. Детерминистские фрактальные решетки обладают такими автомодельными геометрическими свойствами, которые можно использовать при создании быстрого алгоритма формирования ДН, что является очевидным преимуществом при работе с решетками, имеющими большое N. Кроме того, детерминистские фрактальные решетки можно математически рассчитывать с помощью метода, строящегося на системе итерированной функции (СИФ) [12]. В основе СИФ лежит ряд аффинных линейных преобразований, выполняемых в точке (x, y ), находящейся на эвклидовой плоскости. Обычно для решеток с геометриями, основанными на фракталах, такие преобразования описываются тремя локальными параметрами r_n , φ_n , ψ_n и глобальным фрактальным масштабным параметром s_f , так что (см. Ур.1).

Такое определение аффинных линейных преобразований и использование глобального масштабного параметра обеспечивает, что каждый преобразованный объект имеет идентичный масштаб и аналогичен исходному объекту. Ряд Nаффинных линейных преобразований ω₁ , ω₂ ,., ω _N называется оператором Хатчинсона, для которого мы введем символ W . Операцию Хатчинсона можно применять рекурсивно и получить СИФ следующего вида: (см. Ур.2), где фрактал ступени ℓ+1 , (обозначаемый F_ℓ+1 ) строится из фрактала ступени ℓ (обозначаемого F_ℓ ). Последовательные применения оператора Хатчинсона дают все более высоко-порядковые итерации фрактальной структуры.

Другой тип решетки, называемый фрактально-произвольной , сочетает упорядоченные свойства фракталов с неупорядоченными свойствами произвольных решеток. Фрактально-произвольные решетки создаются способом ad hoc (для особого случая), когда генераторы произвольно выбираются из ряда возможных выборов и применяются к фрактальной структуре. Такой произвольный выбор генераторов затрудняет математическое описание этих решеток с помощью СИФ. В целом из малого набора параметров, содержащихся в генераторах, невозможно точно воспроизвести фрактально-произвольные геометрии, и потому они по-настоящему не рекурсивны. Этот факт препятствует использованию рекурсии при создании быстрого алгоритма формирования ДН для такого класса решеток. Тем не менее, благодаря сочетанию упорядоченных и неупорядоченных геометрических свойств, оказалось, что фрактально-произвольные решетки обладают относительно низким уровнем боковых лепестков и в то же время являются устойчивыми. Тем самым такие решетки имеют рабочие характеристики, сочетающие характеристики периодических и произвольных решеток.

Чтобы преодолеть недостатки фрактально-произвольных решеток и одновременно сохранить многие из их желательных свойств, создан особый подкласс фрактально-произвольных решеток, названный ПФР . В предыдущей статье [14] мы разработали новый вид СИФ, способный производить полифрактальные структуры. Аналогично фрактально-произвольным, ПФР строятся из множества генераторов, 1,2,. М , каждый из которых имеет соответствующий оператор Хатчинсона W₁ ,W₂ ,., W_M . Каждый оператор Хатчинсона W_m , в свою очередь, содержит N_m аффинных линейных преобразований ω _m,1 , ω _m,2 ,., ω _{m, N m} . Такие преобразования ω _{m, n} идентичны по форме Ур.1, включая три локальных параметра r_{m , n} , φ_{m , n} , ψ_{m , n} и один глобальный масштабный параметр s_f , который применяется по всей фрактальной структуре (нижний индекс m добавляется для указания на конкретный генератор). Помимо трех локальных параметров здесь введен четвертый локальный κ _{m, n} , который связан с каждым аффинным линейным преобразованием. Этот параметр, называемый показателем связи , является целым значением в пределах от 1 до М , т.е. числа генераторов, используемых для построения ПФР, и применяется для предписания того, как используются аффинные линейные преобразования. Преобразование ω _{m, n} можно выполнить только для тех ПФР ступени ℓ , где генератор, используемый на ступени ℓ , соответствует показателю связи κ _{m, n} . Такая процедура приводит к тому, что с каждым оператором Хатчинсона может быть связана только одна уникальная геометрия ПФР. Следовательно, набор ПФРF_ℓ ступени ℓ можно для удобства выразить в следующей записи (см. Ур.3), где первый нижний индекс определяет уровень ПФР, а второй - генератор, используемый на этом уровне. Отсюда, ПФР ступени ℓ+1 , созданный генератором m , можно представить в виде Ур.4. Чтобы настраивать межэлементное пространство в конфигурации ПФР, мы используем еще один глобальный масштабный параметр s_g . Наконец, отметим, что глобальный масштабный параметр s_f можно вынести (факторизовать) из операторов Хатчинсона, что дает эффективную нормализованную процедуру построения СИФ для ПФР ступени L (см. Ур.5).

Если использовать определение подобия аффинных линейных преобразований так, как это представлено в Ур.1, с добавлением глобальных масштабных коэффициентов и конструкции, основанной на показателе связи, то можно распространить действие быстрых алгоритмов формирования ДН, связанных с обычными фрактальными решетками, на ПФР. Такую широкую методологию формирования ДН, подробно освещенную в [14], можно рассматривать как усовершенствованную СИФ, действующую не на геометрических структурах подгрупп, а на основе их диаграмм направленности. Другими словами, общую ДН можно рассматривать как образуемую решеткой, состоящей из решеток, а не как наложение радиоизлучения, произведенного набором отдельных изотропных точечных источников. В Уравнении 6 дано выражение для конфигурации подгруппы генераторов m ступени ℓ , которое основано на ряде конфигураций фрактальных подгрупп ступени ℓ-1 . Конечную конфигурацию радиоизлучения можно определить, используя изотропные источники для образования ДН исходных подгрупп и рекурсивно применяя данное выражение вплоть до получения ДН ступени L . Рекурсивные свойства формирования ДН, имеющиеся у ПФР, позволяют исследовать в ходе процедуры оптимизации гораздо бо льшие геометрии решеток.

Таким образом, детерминированные фрактальные, полифрактальные и фрактально-произвольные решетки соотносятся друг с другом во многом так, как квадрат с прямоугольником, а прямоугольник с параллелограммом. Фрактально-произвольные решетки обладают наиболее общей геометрией, чем прочие, что в наибольшей степени затрудняет работу с ними. Поскольку в ПФР применяются показатели связи для определения того, как и когда применяется любой из множества генераторов, они являются подклассом фрактально-произвольных решеток. В свою очередь, детерминистские фрактальные решетки по сути являются полифрактальными или фрактально-произвольными решетками, в которых для выбора имеется лишь один генератор. Примеры всех трех типов решеток показаны на Рис.1. Чтобы вам было легче представить конфигурацию решеток, мы используем характерную геометрию фрактального дерева. Кроме того, на Рис.2 для представления отношений, связывающих три типа антенных решеток в плане их конфигурации, использована диаграмма Венна. Параметр S_c представляет поле решения и содержит набор всех возможных методов, используемых для построения антенных решеток.

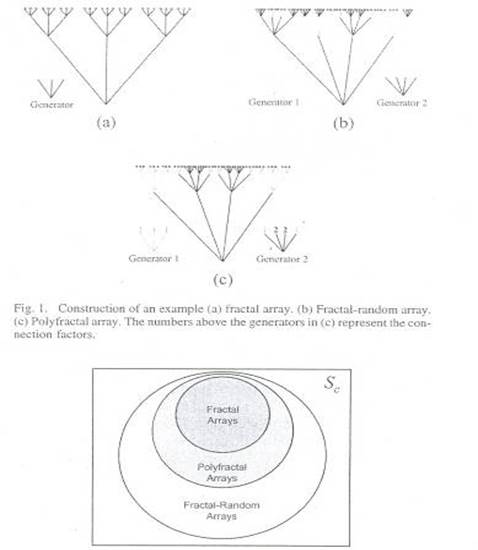
Рис.1. Примеры структур для (а) фрактальной решетки; (b) фрактально-произвольной решетки; (с) ПФР. В (с) цифры, указанные над генераторами, представляют показатели связи.

Рис.2. Диаграмма Венна, показывающая соотношение между фрактальными, полифрактальными и фрактально-произвольными решетками. Поле решения S_c представляет ряд, содержащий все возможные методы построения антенных решеток.

Фрактальные решетки / ПФР / Фрактально-произвольные решетки

генетический алгоритм полифрактальная решетка

Концепции детерминистских фрактальных и полифрактальных решеток можно использовать не только ради их связи друг с другом, но и для описания конфигураций периодических и произвольных решеток. Поскольку ПФР являются подклассом фрактально-произвольных решеток, положения, связанные с ПФР, в равной степени применимы к фрактально-произвольным. Понятия, касающиеся ПФР, можно использовать в описаниях всего ряда периодических антенных решеток, если тщательно подбирать параметры генератора так, чтобы антенные элементы были на равном расстоянии друг от друга. Для решения этой задачи есть несколько способов: возможно, простейшим для понимания является разложенное (факторированное) полифрактальное представление. Возьмем, к примеру, периодическую решетку, полное количество элементов P_T которой можно представить составным числом простых множителей М , так что P_T = р₁ р₂ . р_М . ПФР уровня М можно построить из М генераторов, по одному на каждый из простых множителей. Любой оператор Хатчинсона W_m имеет р _m аффинных линейных преобразований (т.е. N_m = p_m ), когда преобразования выбираются таким образом, чтобы каждая из преобразованных (перенесенных) подгрупп имела периодический интервал. Показатель связи для каждого из этих преобразований равен уровню ℓ фрактально-произвольной решетки, так что каждый из генераторов полностью применяется только к одному-единственному уровню ПФР. Поэтому очевидно, что любая конфигурация периодической решетки должна иметь, по крайней мере, одно соответствие среди ПФР.

Хотя для описания любой периодической решетки можно использовать разложенное полифрактальное представление, могут существовать также и более простые схемы полифрактальных периодических решеток. Разложенное полифрактальное представление можно упростить путем объединения нескольких простых множителей в небольшие составные числа, сокращая тем самым общее количество уровней, необходимых для получения антенной структуры. Более того, хотя и не столь очевидным образом, периодические решетки можно также строить из ПФР более общего характера. Далее, некоторые периодические решетки можно также описывать через детерминистские фрактальные решетки. Помимо тривиального случая одноступенчатой решетки, периодическую решетку можно построить в том случае, когда есть возможность разложить число элементов в структуру N^L , где N представляет число трансформов в операторе Хатчинсона, а L представляет количество ступеней во фрактальной решетке. Параметры определяют так, чтобы интервалы между любыми аффинными линейными преобразованиями оператора Хатчинсона были равны. В Таблице 1 приведены параметры, необходимые для создания N^L -элементной периодической решетки на основе детерминистской фрактальной. На Рис.3 показаны примеры факторированного полифрактального, общего полифрактального и N^L -фрактального представлений периодической решетки.

Таблица 1. Общая конфигурация (хромосома) N^L -элементной периодической решетки, созданная с использованием характерной детерминистской фрактальной геометрии: N^L -элементная периодическая решетка, периодический интервал d Генератор, N – четное, Генератор, N – нечетное, or - или

Рис.3. (а) Факторированное полифрактальное представление; (b) Общее полифрактальное представление; (с) N^L -фрактальное представление периодической решетки. Цифры, указанные над генераторами, являются показателями связи.

Если набор применяемых генераторов столь велик, что ни один из них не может быть выбран более одного раза, методологией ПФР можно пользоваться для описания полностью произвольных решеток. Полифрактальная модель, хотя и является для чисто произвольных решеток громоздкой и неэффективной, с теоретической точки зрения все же вполне здесь применима. Таким образом, можно сделать вывод, что с помощью ПФР можно описать любой класс антенных решеток. Кроме того, в большинстве случаев оказывается, что для решеток, построенных из множества генераторов, разупорядоченность (произвольность) ПФР является бо льшей. Показанная на Рис.4 диаграмма Венна представляет классификацию периодических, произвольных, фрактальных и полифрактальных решеток относительно конечной конфигурации решетки. В поле решения S_a показан ряд всех возможных конфигураций решеток; это поле отличается от поля решения S_с , представленного выше. Из Рис.4 также очевидно, что любую решетку можно представить в виде ПФР. Однако пунктиром обозначена граница, за пределами которой полифрактальную модель больше невозможно использовать для описания геометрии антенной решетки. В данной статье мы предъявляем оптимизационную процедуру, с помощью которой можно, используя понятия, характерные для ПФР, последовательно преобразовывать решетки, имеющие периодическую конфигурацию, основанную на фракталах, в более произвольные решетки. В следующих разделах подробно обсуждаются процессы, используемые для того, чтобы оптимизация могла следовать в этом русле.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--