Статья: Геометрические свойства регулярного круглого конуса в пространстве
1.7. Пусть E – банахово пространство над R со строго регулярным замкнутым конусом Е+. Элементы x, у Î Е+ называются н-дизъюнктными или ортогональными по Роберу (обозначается x ![]() у), если ||x + λу|| = ||x – λу|| для любого λ ≥ 0.
у), если ||x + λу|| = ||x – λу|| для любого λ ≥ 0.
2. Описание множеств |Х|, Х+, Х-
Рассмотрим пространство ![]() , упорядоченное регулярным круглым конусом K(f,a), где a = 0,5 и функционал f имеет первую координату, равную единице, а остальные координаты нулевые:
, упорядоченное регулярным круглым конусом K(f,a), где a = 0,5 и функционал f имеет первую координату, равную единице, а остальные координаты нулевые:
K1 = {x = (x1, x2, ..., xn) : x1 ≥ |x2| + … + |xn|}.
Все результаты легко перенести на общий случай (1) с помощью изометричного преобразования. В дальнейшем, если не указано иное, будем обозначать через X = ![]() .
.
Опишем множества |Х|, Х+, Х- для произвольного элемента x = (x1, ..., xn) Î![]() . Заметим, что частный случай разложения элемента х на ортогональные по Роберу положительную и отрицательную части рассмотрен в [6].
. Заметим, что частный случай разложения элемента х на ортогональные по Роберу положительную и отрицательную части рассмотрен в [6].
2.1. Пусть x1 = 0. Найдем элемент конуса, который мажорирует элементы ± х и равен им по норме, т. е. у = (у1, …, yn) : y1 ≥ ![]() , y ≥ ± х, ||y|| = ||x||. Такой элемент описывает следующая система:
, y ≥ ± х, ||y|| = ||x||. Такой элемент описывает следующая система:
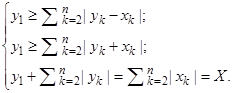
Сложив первые два неравенства, получим оценку у1 ≥ X. С другой стороны, из третьего равенства видно, что у1 ≤ X. Тогда у1 = X, ![]() = 0, следовательно yk = 0 для любого
= 0, следовательно yk = 0 для любого ![]() . Получаем следующее представление метрического модуля элемента х и его положительной и отрицательной части
. Получаем следующее представление метрического модуля элемента х и его положительной и отрицательной части
![]() ,
,
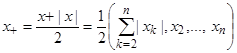 ,
,
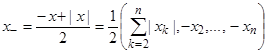 .
.
2.2. Пусть x1 > 0. В этом случае система, описывающая элемент у Î |Х|, имеет вид:
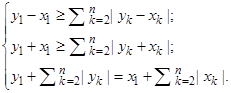
Аналогичные действия позволяют утверждать, что X≤у1≤X + х1, т.е. у1 представим в виде у1 = X + λх1, где 0 ≤ λ ≤ 1. Последовательно подставляя значение у1 в систему, имеем: ![]() -|yk – xk|) ≥ ≥ х1(l – λ) =
-|yk – xk|) ≥ ≥ х1(l – λ) = ![]() , с другой стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге получаем:
, с другой стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге получаем:
|xk| = |yk| + |yk − xk| (![]() ).
).
Из этого равенства следует, что уk и хk – yk – одного знака, что приводит к следующим выводам:
если (xk − yk) > 0 и yk > 0, то 0 < yk < xk ;
если (xk − yk) < 0 и yk < 0, то xk < yk < 0;
если (хк – yk) = 0 и yk = 0, то хk = уk = 0.
Из чего следует, что каждая координата уk (![]() ) представима в виде уk = λkхk, 0 ≤ λk ≤ 1.
) представима в виде уk = λkхk, 0 ≤ λk ≤ 1.
Отметим равенство, используемое в дальнейшем:
 .
.
Итак, при x1 > 0 имеем:
![]()
где  , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()
где  , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()