Статья: Геометрические свойства регулярного круглого конуса в пространстве
4.4. Пусть x1 > 0 и элемент x не принадлежит конусу K1. Если а = (a1, ..., аn) Î М(x), то ||a – x|| = ||x–|| = d(x, К1) = ![]() – x1
– x1
или 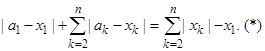
Так как a Î K1 , то а1 ≥ ![]() . Тогда последовательно получаем a1 ≤ |а1 – x1| + x1 =
. Тогда последовательно получаем a1 ≤ |а1 – x1| + x1 = ![]() -
- ![]() ≤
≤ ![]() ≤ a1 , что равносильно системе
≤ a1 , что равносильно системе
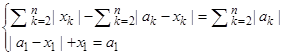
или
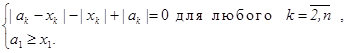
Получаем, что (аk – xk) и xk – одного знака, т. е. аk = akxk, где 0 ≤ ak ≤ 1 для любого ![]() . Подставив в (*), имеем а1 +
. Подставив в (*), имеем а1 + ![]() =
= ![]() .
.
Таким образом, выражение для а1 имеет вид: а1 =![]() .
.
В итоге получаем, что если х1 > 0, то
![]() где 0≤ak≤ 1,
где 0≤ak≤ 1, ![]() }.
}.
4.5. Пусть x1 < 0 и элемент х не принадлежит конусу –К1, т.е. –x1 < ![]() .
.
Если а = (a1, ..., аn) Î М(x), то ||a-x|| = ||x–|| = d(x, К1) =![]() –x1
–x1
или 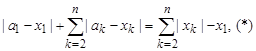
или ![]()
Откуда a1= ![]() -
- ![]() ≥
≥![]() . В то же время
. В то же время ![]() ≥
≥ ![]() +
+ ![]() ≥
≥ ![]() . Из последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого k, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого
. Из последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого k, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого ![]() . Тогда a1=
. Тогда a1=![]() –
–![]() =
=![]() . Получаем, что (4.4) верно и для этого случая.
. Получаем, что (4.4) верно и для этого случая.
5. Описание множества M(x)∩K1
Интересен вопрос о взаимоотношении множества положительных частей элемента и множества элементов, на которых достигается расстояние от элемента до конуса.
Пусть элемент x принадлежит конусу К1. В этом случае М(х) = {x}, а Х+ = {![]() (Х + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤ 1,
(Х + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤ 1, ![]() = x1(1 – λ)}. При λk = 1 получим λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì Х+.
= x1(1 – λ)}. При λk = 1 получим λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì Х+.
Пусть элемент x принадлежит конусу –К1. Если аÎ М(x)∩Х+, то, учитывая формулы 4.2 и 2.2, получим:
![]() (
(![]() + x1(1 – λ), x2(1 – λ2), ... , xn(1 – λn)).
+ x1(1 – λ), x2(1 – λ2), ... , xn(1 – λn)).
Из этого равенства следует, что ![]() ) при λk Î[0,1]. Итак, для любого λk,
) при λk Î[0,1]. Итак, для любого λk, ![]() найдется
найдется ![]() такое, что из того, что а Î Х+ следует, что а Î М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+ .
такое, что из того, что а Î Х+ следует, что а Î М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+ .
5.3. Пусть x1 = 0 и элемент x не принадлежит конусу. Воспользовавшись формулами 4.3 и 2.1, получим М(х) ∩ Х+ = Х+.
5.4. Пусть x1 > 0 и элемент x не принадлежит конусу. Если элемент принадлежит М(х) ∩ Х+ , то выполняется равенство:
![]() (
(![]() + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)),
+ x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)),
что равносильно системе
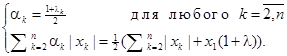
Данные равенства выполняются, если λk такие, что λ = 0. В этом случае ![]() , т.е.
, т.е.
М(x)∩Х+=![]() .
.
5.5. Пусть x1 < 0 и элемент х не принадлежит конусу –К1. Если элемент принадлежит М(х) ∩ Х+ ,то выполняется равенство: