Статья: Интерпретация квантовомеханических представлений с позиций волнового описания системности физических величин

Нормированная волновая функция, получаемая решением уравнения Шредингера для микрочастицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет вид:

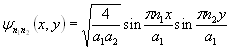, (3.10)

0 < x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, …

Энергия микрочастицы описывается выражением

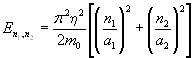, n1, n2 = 1, 2, 3, … (3.11)

Последнее выражение можно упростить и представить по аналогии с (3.8) в виде

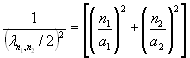, n1, n2 = 1, 2, 3, … (3.12)

Однако из последнего выражения нельзя получить простого соотношения, подобного (3.9). Выражение (3.12) говорит о том, что сложение волн происходит по правилу сложения векторных величин.

Аналогичное выражение для трехмерной потенциальной ямы имеет вид:

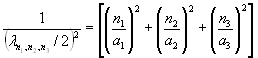, n1, n2, n3 = 1, 2, 3, … (3.13)

Таким образом, можно заключить, что частица, находящаяся в многомерной потенциальной яме с бесконечно высокими стенками, описывается набором стационарных волн, длины которых целочисленно дольны величинам сторон этой потенциальной ямы.

Уравнение Шредингера для частицы, находящейся в сферической потенциальной яме с непроницаемой стенкой радиуса а, имеет решение идентичное (3.3) – (3.5) [1]. Это означает, что в такой потенциальной яме стационарные волны де Бройля состоят из основной волны, половина длины которой равна длине окружности сферы, и бесконечно большого набора других волн, целочисленно дольных основной.

Волновое представление микрочастиц позволяет описывать их проникновение в стенки потенциальных ям и прохождение сквозь потенциальные барьеры конечной высоты. Свободное движение частицы в области, где уровень потенциальной энергии меньше уровня кинетической энергии, описывается уравнением (3.1). Его решение, записанное в показательной форме, имеет вид:

. (3.14)

В области потенциального порога или стенки потенциальной ямы, где потенциальная энергия превышает уровень кинетической энергии (U-E) > 0 волновое уравнение имеет другой вид:

. (3.15)

Решением этого уравнения является сумма двух экспонент с действительными показателями степеней

(3.16)

В результате сшивки двух функций (3.14) и (3.16) с учетом требований конечности и гладкости, предъявляемых к пси-функции, коэффициент А2 принимается равным нулю, коэффициент А1 принимается равным единице и определяются значения коэффициентов В1 и В2.

При прохождении микрочастицы над низким потенциальным порогом (E – U) >0 тоже наблюдается отражение. При этом уравнение Шредингера в любой зоне имеет вид (3.1), решения уравнения предстают в виде (3.14), а коэффициенты получают значения:

А1 = 1, В2 = 0, и . (3.17)

Квадрат коэффициента В1 представляет собой коэффициент отражения R частицы от высокого потенциального порога, а квадрат коэффициента А2, представляет собой коэффициент прозрачности D, причем D = 1 – R.

Думается, что коэффициент прозрачности прямоугольного потенциального барьера, обычно представляемый в виде

(3.18)

лучше записывать по иному, в виде:

. (3.19)

Такая форма представления не только понятнее, но и проще для запоминания. Выражение (3.19) говорит и о том, что высокочастотные составляющие волновой функции проходят потенциальные барьеры с большими потерями. То есть волновые свойства микрочастицы, попадающей внутрь потенциальной стенки или потенциального барьера, становятся качественно иными. По-видимому, имеет место также и качественно иное изменение микрочастиц, при преодолении ими потенциального порога и освобождении из связанного состояния, например для электронов, покидающих атом.

4. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА, ИХ СИСТЕМНОЕ ПРЕДСТАВЛЕНИЕ И РАЗВИТИЕ

Известные соотношения неопределенностей, сформулированные Вернером Гейзенбергом,