Статья: Краткое доказательство великой теоремы Ферма
Великая теорема Ферма формулируется следующим образом: диофантово уравнение (http://soluvel.okis.ru/evrika.html):
А n + В n = С n * /1/
где n - целое положительное число, большее двух, не имеет решения в целых положительных числах A , B , С .
ДОКАЗАТЕЛЬСТВО
Из формулировки Великой теоремы Ферма следует: если n – целое положительное число, большее двух, то при условии, что два из трех чисел А , В или С - целые положительные числа, одно из этих чисел не является целым положительным числом.
Доказательство строим, исходя из основной теоремы арифметики, которая называется «теоремой о единственности факторизации» или «теоремой о единственности разложения на простые множители целых составных чисел». Возможны нечетные и четные показатели степени n . Рассмотрим оба случая.
1. Случай первый: показатель степени n - нечетное число.
В этом случае выражение /1/ преобразуется по известным формулам следующим образом:
А n + В n = С n = (A+B)[An-1 -An-2 ·B +An-3 ·B2 - …-A·Bn-2 +Bn-1 ] /2/
Полагаем, что A и B – целые положительные числа.
Числа А , В и С должны быть взаимно простыми числами.
Из уравнения /2/ следует, что при заданных значениях чисел A и B множитель ( A + B ) имеет одно и тоже значение при любых значениях показателя степени n , следовательно, он является делителем числа С.
Допустим, что число С - целое положительное число. С учетом принятых условий и основной теоремы арифметики должновыполняться условие:
С n = An + Bn =(A+B)n ∙ Dn , / 3/
гдемножитель Dn должен быть целым числом и, следовательно, число D также должно быть целым числом.
Из уравнения /3/ следует:
![]() /4/
/4/
Из уравнения /3/ также следует, что число [Cn = An + Bn ] при условии, что число С – целое число, должно делиться на число ( A + B ) n . Однако известно, что:
An + Bn < ( A + B ) n /5/
Следовательно:
![]() - дробное число, меньшее единицы. /6/
- дробное число, меньшее единицы. /6/
![]() - дробное число.
- дробное число.
Отсюда следует, что при нечетном значении показателя степени n уравнение /1/ великой теоремы Ферма не имеет решения в целых положительных числах.
При нечетных показателях степени n >2 число:
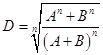 < 1- дробное число, не являющееся рациональной дробью.
< 1- дробное число, не являющееся рациональной дробью.
Из анализа уравнения /2/ следует, что при нечетном показателе степени n число:
С n = А n + В n = (A+B)[An-1 -An-2 ·B +An-3 ·B2 - …-A·Bn-2 +Bn-1 ]
состоит из двух определенных алгебраических множителей, при этом при любом значении показателя степени n неизменным остаетсяалгебраический множитель ( A + B ).
Таким образом, великая теорема Ферма не имеет решения в целых положительных числах при нечетном показателе степени n >2.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--