Статья: Краткое доказательство великой теоремы Ферма
Суть великой теоремы Ферма не изменится, если уравнение /1/ перепишем следующим образом:
An = Cn - Bn /7/
В этом случае уравнение /7/ преобразуется следующим образом:
An = Cn - Bn = ( С +B)∙(Cn-1 + Cn-2 · B+ Cn-3 ∙ B2 +…+ C ∙ Bn -2 + Bn -1 ). /8/
Принимаем, что С и В – целые числа.
Из уравнения /8/ следует, что при заданных значениях чисел B и C множитель (С+ B ) имеет одно и тоже значение при любых значениях показателя степени n , следовательно, он является делителем числа A .
Допустим, что число А – целое число. С учетом принятых условий и основной теоремы арифметики должновыполняться условие:
А n = С n - Bn =(С+ B ) n ∙ Dn , / 9/
гдемножитель Dn должен быть целым числом и, следовательно, число D также должно быть целым числом.
Из уравнения /9/ следует:
![]() /10/
/10/
Из уравнения /9/ также следует, что число [А n = С n - Bn ] при условии, что число А – целое число, должно делиться на число (С+ B ) n . Однако известно, что:
С n - Bn < (С+ B ) n /11/
Следовательно:
![]() - дробное число, меньшее единицы. /12/
- дробное число, меньшее единицы. /12/
![]() - дробное число.
- дробное число.
Отсюда следует, что при нечетном значении показателя степени n уравнение /1/ великой теоремы Ферма не имеет решения в целых положительных числах.
При четных показателях степени n >2 число:
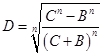 < 1- дробное число, не являющееся рациональной дробью.
< 1- дробное число, не являющееся рациональной дробью.
Таким образом, великая теорема Ферма не имеет решения в целых положительных числах и при четном показателе степени n >2.
Из изложенного следует общий вывод: уравнение /1/ великой теоремы Ферма не имеет решения в целых положительных числах А, В и С при условии, что показатель степени n >2.
ДОПОЛНИТЕЛЬНЫЕ ОБОСНОВАНИЯ
В том случае когда показатель степени n – четное число, алгебраическое выражение (Cn - Bn ) раскладывается на алгебраические множители:
C2 – B2 = (C-B) ∙ (C+B); /13/
C4 – B4 = ( C-B) ∙ (C+B) (C2 + B2 );/14/
C6 – B6 = (C-B) ∙ (C+B) · (C2 –CB + B2 ) ∙ (C2 +CB+ B2 ); /15/
C8 – B8 = (C-B) ∙ (C+B) ∙ (C2 + B2 ) ∙ (C4 + B4 )./16/
Приведем примеры в числах.
ПРИМЕР 1: В=11; С=35.