Статья: Нелокальная краевая задача для уравнения смешанного типа третьего порядка с кратными характерис
Учитывая (15) в равенстве (7), будем иметь:
(16)
где обозначено 
(17)
|
(18)
(19)
Введем вспомогательную функцию 
по формуле :
(20)
Легко заметить, что функция 
и в точке x=0 обращается в нуль порядка выше e, а при x=1 может обращаться в бесконечность порядка выше (1-e) относительно x и (1-x) соответственно. Из равенства (20) однозначно определяется функция 
:
(21)
Учитывая значение функции 
из равенства (21), в интегралах в правой части (16) получаем:
.
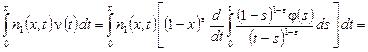
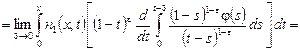
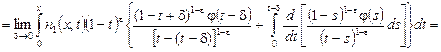
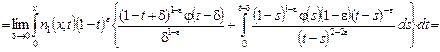
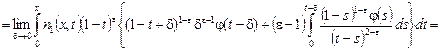
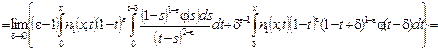
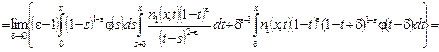
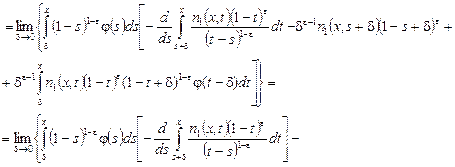
Обозначим
. (22)
Тогда окончательно имеем:
.
Аналогично находим, что
,