Статья: Нелокальная краевая задача для уравнения смешанного типа третьего порядка с кратными характерис

; (24)

. (25)

Используя известное тождество [3],

,

где интеграл понимается в смысле главного значения по Коши, уравнение (16) с учетом (5`), (17) – (19), (22) – (25) и делая несложные преобразования, приводится к сингулярному интегральному уравнению [1, 3]:

(26)

где сингулярный оператор S задаётся формулой:

,

, ,

,

, , – известные функции, ограниченные соответственно на 0 £ t £ x £ 1, 0 £ x £ t £ 1, 0 £ x £ 1, причем , .

Производя регуляризацию уравнения (26) по методу Карлемана – Векуа [4] и делая несложные преобразования, оно приводится к интегральному уравнению Фредгольма третьего рода [2]:

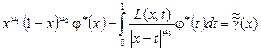, (27)

где причем ядро и функция ограниченные соответственно при, 0£ x, t£ 1, 0£ x£ 1.

Следуя [2], обозначим через – множество функций , непрерывных всюду кроме быть может точек x=0, (x=1) и удовлетворяющих условию где , – целая часть , – целая часть [1].

В работе [2] найдены необходимые и достаточные условия существования решения уравнения (27) в классе .

Функция , определенная формулой (21), принадлежит классу искомых решений интегрального уравнения (8).

После определения , функция задаётся формулой (12). Таким образом, в области приходим к задаче [6]: найти регулярное в области решение уравнения (1), непрерывное вместе с производной в замкнутой области и удовлетворяющее граничным условиям (4) и .

Решение этой задачи задается формулой :

где – функция Грина этой задачи для уравнения

. (28)

Функция Грина выражается через фундаментальные решения уравнения (28), которые имеют вид:

где ;

;

– функция Бесселя. Функции , называются функциями Эйри и удовлетворяют уравнению . Основные свойства функций и , их оценки вместе с частными производными порядка больше 1, приведены в [7].

Список литературы