Математика / Статья: Нелокальная краевая задача для уравнения смешанного типа третьего порядка с кратными характерис

Статья: Нелокальная краевая задача для уравнения смешанного типа третьего порядка с кратными характерис

В работе рассматривается нелокальная краевая задача для уравнения смешанного типа. Поставленная задача сводится к сингулярному интегральному уравнению, которое методом Карлемана-Векуа редуцируется к интегральному уравнению Фредгольма третьего рода.

Рассмотрим уравнение

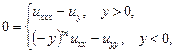(1)

где m – натуральное число в конечной односвязной области , ограниченной отрезками прямых соответственно – и характеристиками:

уравнения (1).

Пусть ;– интервал прямой ;

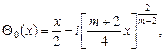
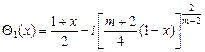
– аффиксы точек пересечения характеристик уравнения (1) при , выходящих из точки , с характеристиками и соответственно;

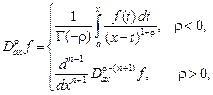(2)

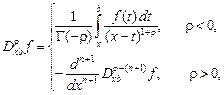(3)

– операторы дробного интегрирования порядка - при и обобщенные в смысле Лиувилля производные порядка при , причем

где – единичный оператор, а – целая часть .

Под регулярным в области решением уравнения (1) будем понимать функцию , удовлетворяющую уравнению (1) в , и такую, что может обращаться в бесконечность порядка ниже на концах А и В интервала I.

Задача Н. Найти регулярное в области решение уравнения (1), удовлетворяющее краевым условиям:

, (4)

, (5)

где ,

(5`)

. (6)

Пусть существует решение задачи . Тогда, регулярное решение уравнения (1) в гиперболической части , удовлетворяющее данным Коши , дается формулой [1]: