Учебное пособие: Дифференциальное уравнение теплопроводимости

На практике приходится иметь дело с температурными полями, обладающими специальными свойствами симметрии, облегчающими изучение таких полей.

§ 2.3 Температурный градиент

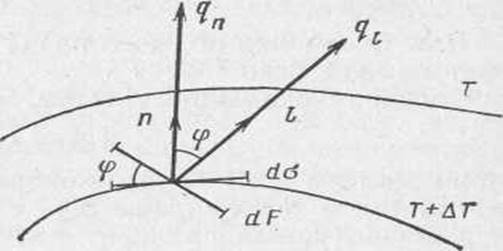
Рассмотрим две бесконечно близкие изотермические поверхности
с температурами Т и Т+∆Т(∆Т>0) и какую-либо точку М, лежащую
на одной из них (рис. 2.3).

Рис. 2.3

Перемещаясь из точки М вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться вдоль какого либо направления l, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры Т при переходе от точки М к близкой точке М' по направлению l. Скорость изменения температуры Т в точке М в направлении l характеризуется производной функции Т

дТ/дl= lim[T(M’) - Т(М)]/∆l. (2.3)

∆l→0

Наибольшая разность температуры на единицу длины вектора перемещения [Т(М")—Т(М)]/∆l наблюдается в направлении нормали n к изотермической поверхности (рис. 2.3). В соответствии с (2.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры ∆T к расстоянию между изотермическими поверхностями по нормали ∆n, когда ∆n стремится к нулю:

дТ/дп= lim [T(M")—T(M)]/∆n= lim ∆T/∆n. (2.4)

∆n →0 ∆n →0

Итак, в любой точке М изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единицу длины перемещения в рассматриваемом направлении — скорости возрастания температуры в этом направлении (т. е. производной от температурной функции Т по направлению нормали n). Такой вектор называют градиентом температуры в точке М или градиентом температурного поля и записывают в виде символа grad T:

в декартовых координатах (х, у, z)

grad T = ∂T/∂x i + ∂T/∂y j + ∂T/∂z k (2.5)

Для обозначения вектора (2.5) в теории поля иногда применяют символ gradT = T

Согласно сказанному выше, можно записать

|grad T| = ∂T/∂n (2.6)

длина вектора grad Т равна скорости возрастания Т в этом направлении. Здесь и всюду далее n — единичный вектор нормали.

Температурный градиент показывает, насколько интенсивно (резко) меняется температура внутри тела.

Производная от функции Т по направлению нормали n и вектор gradT связаны соотношением

дТ/дп = п grad Т. (2.7)

Вектор нормали n к поверхности T=const в точке М может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним.

Если нормаль n направить в сторону больших температур, то дТ/дп>0 и, как следует из (2.7), градиент температуры будет направлен в ту же сторону (угол между векторами n и grad T равен нулю). Если нормаль направить в сторону убывающей температуры, то производные дТ/дп < 0 и gradT окажутся направленными противоположно этому направлению, т. е. опять в сторону возрастающей температуры.

Тепловой поток. Векторная и скалярная формы закона Фурье

В теле, не находящемся в полном тепловом равновесии (т. е. обладающим неравномерным распределением температуры), всегда происходит перенос теплоты. Отсюда следует, что для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела. Тепловой поток в отличие от температуры — величины скалярной — имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как ректор, направленный в сторону уменьшения температур, а поле тепловых потоков — векторным. Для математического описания поля тепловых потоков вводится вектор q, называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке М температурного поля понимают вектор, направление которого совпадает с направлением переноса теплоты, а абсолютная величина выражает тепловой поток или интенсивность переноса теплоты, измеряемую количеством теплоты, проходящей в единицу времени через единицу площади поверхности, перпендикулярной направлению потока в рассматриваемой точке. Обозначим через dQ количество теплоты, проходящее через изотермическую поверхность площади dσ за время dt. Тогда, по определению, абсолютное значение вектора плотности теплового потока можно записать в виде

q = dQ/ (dσ dt) (2.8)

Формула (2.8) характеризует плотность теплового потока единичного элемента изотермической поверхности. Понятие плотности теплового потока, как будет показано ниже, применимо к любой, а не только к изотермической поверхности.

Опыт показывает, что передача теплоты теплопроводностью происходит по нормали к изотермической поверхности от мест с большей температурой к местам с меньшей температурой. Следовательно, вектор плотности теплового потока направлен по нормали к изотермической поверхности в направлении падения температуры. Можно говорить о плотности теплового потока и вдоль любого другого направления l, отличного от направления нормали п. В этом случае плотность теплового потока в направлении l есть проекция вектора q на это направление, т.е. величина q·cos(n,l).

Сущность гипотезы Фурье состоит в том, что тепловой поток через элемент изотермической поверхности вполне определяется значением температурного градиента в рассматриваемой точке М. Возникновение тепловых потоков вдоль изотермических поверхностей невозможно, так как по всей изотермической поверхности составляющая градиента температуры равна нулю. Следовательно, векторы плотности теплового потока q и grad T направлены по нормали к изотермической поверхности, но в противоположные стороны (рис. 2.4).

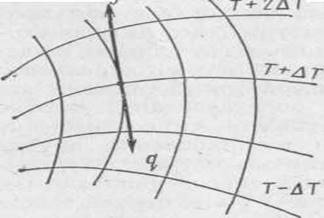
Рис. 2.4