Учебное пособие: Дифференциальное уравнение теплопроводимости

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ

Общие вопросы теории теплообмена

Неравномерное распределение температуры в металле, характерное для сварки и других видов местной тепловой обработки металла, неустойчиво. С течением времени температура в неравномерно нагретом теле выравнивается, причем более нагретые части отдают тепло непосредственно соприкасающимся с ними менее нагретым частям. Такой энергетический обмен между взаимодействующими телами или их отдельными частями с неодинаковой температурой называется теплообменом или теплопередачей. Количество энергии, переданной частицами более горячего тела частицам более холодного, называется количеством теплоты, или просто теплотой. При этом теплота переходит от точек с более высокой температурой к точкам с более низкой температурой, если процесс протекает в одном теле. При теплообмене между различными телами это положение также сохраняется, т. е. теплота переходит от более нагретых к более холодным телам. Таким образом, конечный результат теплообмена между ограниченными телами или частями одного и того же тела заключается в уравнивании их температур, после чего процесс прекращается.

Понятие «теплообмен» охватывает совокупность всех явлений, при которых имеет место перенос некоторого количества теплоты из одной части пространства в другую в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений. Для удобства принято делить перенос теплоты на простейшие виды: теплопроводность, конвекцию, теплообмен излучением, или радиацией. Эти процессы глубоко различны по своей природе и характеризуются различными законами. Соответственно этому и строится математическая теория описания каждой формы теплообмена, со своими уравнениями, своими математическими методами, аналитическими или численными, или методами аналогий.

Теплопроводность характеризуется тем, что ее действие связано с наличием вещественной среды и что теплообмен может происходить только между такими частицами тела (молекулами и атомами), которые находятся в непосредственной близости друг от друга. Явление это можно представить себе так, что теплота переходит от одной частицы к другой, однако при этом сами частицы не перемещаются. В чистом виде процесс теплопроводности наблюдается в твердых телах.

Конвекция наблюдается тогда, когда материальные частицы какого-нибудь тела изменяют свое положение в пространстве и при этом переносят содержащуюся в них теплоту. Это явление имеет место в жидкостях и газах и всегда сопровождается теплопроводностью, т. е. передачей теплоты от одной частицы к соседней, если только во всей текущей массе нет полного равенства температур. Теплообмен между средой и стенкой называют теплоотдачей.

Теплообмен излучением характеризуется отсутствием контакта между телами, обменивающимися теплотой. Примером может служить излучение Солнцем теплоты на Землю через космическое пространство, в котором, как известно, плотность вещества ничтожна. Явление теплового излучения возникает у поверхности или внутри тела в результате сложных молекулярных и атомных возмущений. При этом некоторая часть внутренней энергии тела преобразуется в электромагнитные волны (или в другом представлении в фотоны — кванты энергии) и уже в такой форме передается через пространство.

Все эти различные формы переноса теплоты не обособлены и в чистом виде встречаются лишь на отдельных участках пути прохождения теплоты. В большинстве случаев один вид теплообмена сопутствует другому и разделить их между собой очень трудно.

Одним из законов, лежащих в основе аналитической теории теплопроводности, является гипотеза Фурье, связывающая перенос теплоты внутри тела с температурным состоянием в непосредственной близости от рассматриваемого места. Поэтому при изучении теории теплопроводности прежде всего необходимо установить основные понятия, такие, как температурное поле, градиент температуры, вектор теплового потока.

Температурное поле

Температурным полем называется совокупность значений температуры во всех точках рассматриваемого пространства (тела) в каждый фиксированный момент времени.

Температура является скалярной величиной, так как она характеризует тепловое состояние в любой точке тела, определяя степень его нагретости. Температуре нельзя приписать какое-либо направление и поэтому температурное поле является скалярным. Математическим выражением распределения температуры в теле является выражение, содержащее в качестве независимых переменных пространственные координаты и время:

в декартовой системе координат

Т=Т(х,у,z,t); (2.1)

Основной задачей аналитической теории теплопроводности является изучение пространственно-временного изменения температуры, т. е. нахождение зависимости (2.1). Уравнение (2.1) является записью наиболее общего вида температурного поля, когда температура в теле изменяется с течением времени и от одной точки к другой. Такое поле соответствует неустановившемуся тепловому режиму теплопроводности и называется нестационарным температурным полем. Если тепловой режим является установившимся, то температура в каждой точке тела с течением времени остается неизменной, меняясь лишь от точки к точке. Такое температурное поле называется стационарным и температура является функцией только координат, например в декартовых координатах

Т=Т(х, у, z), ∂T/∂t=0. (2.2)

Температурное поле, соответствующее уравнению (2.2), является пространственным, или трехмерным, так как температура является функцией трех координат.

Если вдоль одной из координат температура остается постоянной, то математически это условие записывается (например, для координаты z) следующим образом: дТ/дz=0. В этом случае поле называется двумерным и записывается: для нестационарного режима Т=Т(х, у, t); для стационарного режима Т=Т(х, у).

Если температура остается постоянной вдоль двух координат (например, у и z), то дТ/ду = дТ/дz = 0 и поле называется одномерным. В этом случае можно записать: для нестационарного режима Т=Т(х, t); для стационарного Т=Т(х).

Переменные х, у, z, фигурирующие в уравнении (2.1), определяют положение любой точки рассматриваемого тела, являясь координатами этой точки в выбранной системе координат. Эти переменные могут принимать бесконечное множество числовых значений, как и переменная t, характеризующая время течения процесса теплопроводности. Совокупность всевозможных числовых значений переменных х, у, z, t, каждому из которых соответствует вполне определенное значение температуры Т=Т(х, у, z, t), называется областью определения функции Т(х, у, z, t). Функция Т(х, у, z, t) в своей области определения считается обычно непрерывной, дважды непрерывно дифференцируемой по пространственным координатам (х, у, z) и непрерывно дифференцируемой по времени t.

В теле, имеющем температуру Т(х, у, z, t), можно выделить поверхность, во всех точках которой в некоторый момент времени температура одинакова. Такая поверхность называется изотермической поверхностью или поверхностью уровня. Уравнение поверхности уровня имеет следующий вид:

Т(х, у, z, t)=C или Т=С, где C=const.

В отличие от стационарных в нестационарных полях форма и расположение изотермических поверхностей с течением времени изменяются. Изотермические поверхности характеризуются следующими основными свойствами:

а) две изотермические поверхности, имеющие различные температуры, никогда не пересекаются друг с другом, так как в одной и той же
точке тела одновременно не может быть двух различных температур;

б) изотермические поверхности не имеют границ внутри тела. Они
или кончаются на поверхности, или замыкаются на себя, располагаясь
внутри тела;

в) теплота не распространяется вдоль изотермической поверхности,
а направляется от одной изотермической поверхности к другой. Это следует из положения о том, что тепловая энергия распространяется от более нагретого участка к менее нагретому.

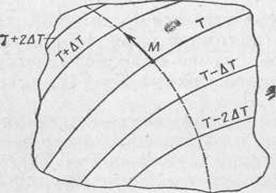
Рис. 2.1

Таким образом, можно считать, что изотермические поверхности разделяют твердое тело на тонкие «слои» — изотермические оболочки, отделяющие часть тела с температурой, большей, чем T=С, от части тела с температурой, меньшей, чем Т=С. Пересечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм (линии, соответствующие одинаковой температуре). Они обладают теми же свойствами, что и изотермические поверхности, т. е. не пересекаются, не обрываются внутри тела, оканчиваются на поверхности либо целиком располагаются внутри самого тела. На рис. 2.1 представлен участок двумерного температурного поля с изотермами Т, Т±∆Т, Т±2∆Т и т. д.

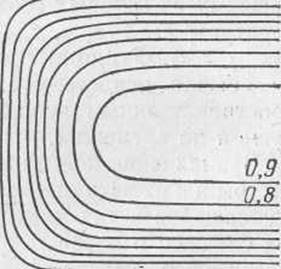
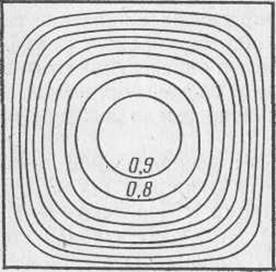
Задание температурного поля соотношением Т=Т(х, у, z, t) не всегда дает достаточно ясное представление о поведении этого поля, а задание изотермических поверхностей (поверхностей уровня) с отметкой на них соответствующих значений температуры Т=С равносильно заданию самого поля Т=Т(х, у, z, t), при этом взаимное расположение поверхностей уровня даст наглядное представление о соответствующем поле температур. Указанный способ изображения поля особенно удобен, когда речь идет о двумерном поле.

Равенство вида Т(х, у, t) = C (всюду время t фиксировано) определяет на плоскости (х, у) некоторую кривую у = φ(х, с, t). Такие кривые называются линиями уровня (изотермами) плоского (двумерного) температурного поля Т=Т(х, у, t) (рис. 2.2).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--