Учебное пособие: Дія магнітного поля на рухомі заряди та закон повного струму і його використання

.

Аналогічно обчислюється індукція магнітного поля, створена іншими провідниками з струмом.

2. ЗАКОН ПОВНОГО СТРУМУ ТА ЙОГО ВИКОРИСТАННЯ ДЛЯ РОЗРАХУНКУ МАГНІТНИХ ПОЛІВ. ВИХРОВИЙ ХАРАКТЕР МАГНІТНОГО ПОЛЯ

У електростатиці було встановлено, що робота при переміщенні одиничного пробного заряду в електричному полі не залежить від форми шлязу і по довільному замкненому контуру дорівнює нулю. Такі поля називають потенціальними. Математична умова потенціальності поля записується у вигляді рівності нулю циркуляції вектора , . Ця умова вказує на те, що силові лінії електростатичного поля незамкнені: починаються на позитивних зарядах і закінчуються на негативних, або прямують у нескінченість.

Виникає запитання, а який характер має магнітне поле? Чи потенціально воно? Щоб відповісти на це обчислимо циркуляцію вектора індукції магнітного поля -?

Хай магнітне поле створюється нескінченно довгим провідником із струмом І (рис.4- переріз провідника, перпендикулярного площині рисунка).

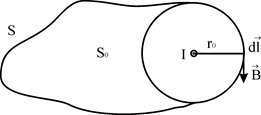
Рис. 4

Для спрощення розрахунків розглянемо найбільш простий випадок: за контур інтегрування S_o оберемо концентричне коло радіуса r_o . Тоді

.

Так як у всих точках кола кут між і дорівнює нулю, то .

а . Отже , а . Тому

( 6 )

Якщо взяти будь-який контур S , то ускладняться обчислення, а результат буде таким же (6).

Якщо контур охоплює декілька провідників із струмами, то циркуляція вектора індукції магнітного поля визначається алгебраїчною сумою струмів охоплених контуром. За принципом суперпозиції , отже

( 7 )

При цьому позитивним вважається такий струм напрям якого зв’язаний з напрямком обходу контура правилом правого гвинта, а струм протилежний напрямку вважається негативним. Наприклад, для випадку, показаному на рис.5 маємо:

Рис. 5

На практиці в розрахунках магнітних кіл часто користуються циркуляцією вектора напруженості магнітного поля . Оскільки для вакууму , то

( 8 )

Закон, який виражається рівностями (7) або (8) називають законом повного струму. Він справедливий для довільних струмів і формулюється так: циркуляція вектора напруженості магнітного поля постійних струмів по довільному замкненому контуру дорівнює алгебраїчній сумі струмів, які охоплюються цим контуром.

Отже, робота при перенесенні пробного одиничного елемента струму в магнітному полі в загальному випадку не дорівнює нулю.

Такі поля називаються не потенціальними, або вихровими, їх не можна характеризувати потенціалом. Силові лінії магнітного поля не мають ні початку ні кінця, тобто вони завжди замкнені або прямують у нескінченність. В цьому полягає одна із відмінностей магнітного поля порівняно з електричним.

Закон повного струму має для розрахунків магнітних полів постійного струму таке ж важливе значення, як теорема Остроградського-Гаусса для розрахунку електростатичних полів.

Розглянемо використання закону повного струму для розрахунку магнітного поля.

1.Обчислимо напруженість магнітного поля на осі нормального соленоїда.

Соленоїдом називають сукупність спірально намотаних на циліндричну поверню витків ізольованого провідника, по якому проходить електричний струм. Як правило, вважають, що провідник намотаний в один шар щільно рівномірно і кількість витків обмотки на одиницю довжини поверхні є величиною сталою і дорівнює , де N –загальна кількість витків, l - довжина намотки соленоїда. Якщо довжина соленоїда більше ніж у 10 разів перевищує діаметр витків, то такий соленоїд називають нормальним.