Учебное пособие: Дискретная математика
Нормальные формы представления переключательной функции иногда называют стандартными (табл. 5).
Таблица 5
| f |
A 0011 B 0101 | Название функции | Обозначение функции | СДНФ | СКНФ |
| f0 | 0000 | Константа нуль | 0 | Не имеет |  |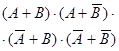
| f1 | 0001 | Логическое произведение, конъюнкция |  | |  |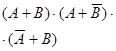
| f2 | 0010 | Функция запрета по В |  | |  |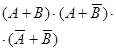
| f3 | 0011 | Переменная А |  |  |  |
| f4 | 0100 | Функция запрета по А |  |  |  |
| f5 | 0101 | Переменная В |  |  |  |
| f6 | 0110 | Сумма по мо дулю 2, логическая неравнозначность |  |  |  |
| f7 | 0111 | Логическое сложение, дизъюнкция |  |  | |
| f8 | 1000 | Операция (стрелка) Пирса, операция Вебба |  | |  |
| f9 | 1001 | Эквивалентность, логическая равнозначность | |  |  |
| f10 | 1010 | Инверсия В |  |  |  |
| f11 | 1011 | Импликация от В к А |  |  |  |
| f12 | 1100 | Инверсия А |  |  |  |
| f13 | 1101 | Импликация от А к В |  |  |  |
| f14 | 1110 | Операция (штрих) Шеффера |  |  |  |
| f15 | 1111 | Константа единица | 1 |  | Не имеет |
Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени.
Теорема. Любая функция булевой алгебры может быть представлена, и притом единственным образом, с помощью полинома Жегалкина вида
J =
.
Представим, например, в виде полинома выражение вида X 1 
X 2 . Для этого проведем следующие рассуждения.
Пусть
X1 X2 = aX1 X2 +bX1 +cX2 +k,
где а, b , с, k – неопределенные коэффициенты.
При X 1 = X 2 = 0 имеем k = 0. При Х1 = 1, X 2 = 0 имеем b = 1. При Х1 = 0, Х2 = 1 имеем с = 1. При X 1 =Х2 = 1 имеем а + b + с = 1, т. е. а = -1. Таким образом, получаем:
X 1 X 2 = – X 1 X 2 + X 1 + X 2 .
СПНФ образуется путем замены в СДНФ: на + и 
на
1 
х.
,
,
В последнем случае выражение для 
легко можно упростить, если раскрыть скобки и взаимно сократить все одинаковые слагаемые, входящие в форм