Учебное пособие: Дискретная математика

.

4. Правило склеивания. Базируется на понятии соседних конъюнкций. Соседними называются конъюнкции, отличающиеся представлением одной переменной. Например, конъюнкции и , и являются попарно соседними. В первой паре конъюнкции отличаются представлением х ₂ , а во второй – представлением х₁ . По этим переменным конъюнкции склеиваются.

Формулировка правила: две соседние конъюнкции склеиваются с образованием одной конъюнкции меньшего ранга; исчезает та переменная, по которой конъюнкция склеивается.

, .

Контрольные вопросы

1. Перечислите основные законы алгебры логики. Как дозывается их справедливость?

2. Перечислите следствия из законов алгебры логики.

3.5 Логические функции многих переменных

Все логические операции, которые были рассмотрены в 3.2, распространяются и на функции нескольких переменных. Теперь будем рассматривать функции F ( x ₁ , x ₂ ,…, x_n ) , где x_i – логические переменные, которые принимают значения нуля или единицы. Для описания логики функционирования аппаратных и программных средств компьютера используется алгебра логики, или булева алгебра. Два элемента алгебры логики – ее константы – 0 (ложь) и 1 (истина). Во всех компьютерах используются сигналы двух видов. Сигналы можно интерпретировать как двоичные числа, или логические переменные.

Логической функцией F от набора логических переменных х₁ ,…, х _n называется функция, которая может принимать только два значения: логический 0 и логическая 1.

Область определения логической функции конечна и зависит от количества возможных наборов аргументов. Если n – число аргументов, то количество возможных наборов аргументов равно 2ⁿ .

Множество значений функции F ( x ₁ ,…, x_n ) – это множество {0,1}, т. е. F =0 либо 1.

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются наборы аргументов, а в правой – соответствующие значения функции.

x1	x2	…	xn-1	xn	F(x1, x2,… , xn-1, xn )
0	0	…	0	0	F (0,0,…, 0,0)
0	0	…	0	1	F (0,0,…, 0,1)
0	0	…	1	0	F (0,0,…, 1,0)
…	…	…	…	…	…
1	1	…	1	1	F (1,1,…, 1,1)

Вектором значений булевой функции F ( x ₁ ,…, x_n ) называется упорядоченный набор всех значений функции F , при которых значения упорядочены по лексикографическому порядку множества аргументов {0,1}ⁿ .

Поскольку всего имеется 2ⁿ наборов нулей и единиц (|{0,1}ⁿ |=2ⁿ ), существует ровно булевых функций F ( x ₁ ,…, x_n ) от n переменных:

.

При n =2 количество функций равно 16, при n =3 – 256 и т. д. На рис. 3 представлены в упорядоченном виде наборы аргументов для ряда функций – отрицания 0, функций одного, двух и трёх аргументов.

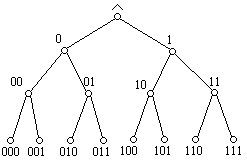
Рис. 3. Упорядоченные наборы аргументов

3.6 Построение формул алгебры логики по заданной таблице истинности

Пусть F – двоичная функция от n переменных. Предположим, что F не равна тождественно нулю. Пусть T ₁ , T ₂ , …, T_k – все точки ее определения, в которых F =1. Можно доказать, что справедлива следующая формула:

,

где , j=1,2,…, k,

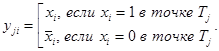
Построить функцию F можно и по-другому. Если функция F не равна тождественно единице и S ₁ , S ₂ ,…, S_m – все точки области ее определения, в которых F =0, то справедлива формула:

,

где , j =1,2,…, m .

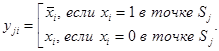
Из приведенных формул видно, что любую двоичную функцию можно записать, используя лишь операции ¬, , .

Основная конъюнкция – это конъюнкция основных высказываний переменных или их отрицаний. Например, .

Основная дизъюнкция – это дизъюнкция основных высказываний переменных или их отрицаний. Например, .