Учебное пособие: Додавання гармонічних коливань та затухаючі коливання

Закон затухаючих коливань визначається властивостями коливальних систем. Звичайно розглядають лінійні системи – ідеалізовані реальні системи.

Лінійними системами являються, наприклад, пружинні маятники при малому розтягуванні пружини (коли слушний закон Гука), коливальний контур, індуктивність, ємність і опір якого не залежить ні від струму в контурі, ні від напруги.

Різні по своїй природі лінійні системи описуються ідентичними лінійними диференціальними рівняннями, що дозволяє підходити до вивчення коливань різної фізичної природи з єдиної точки зору, а також проводити їх моделювання, в тому числі і на ЕВМ.

Диференціальне рівняння вільних затухаючих коливань лінійної системи задається у вигляді:

,

де S – коливальна величина, що описує той чи інший фізичний процес,

d - const - коефіцієнт затухання,

- циклічна частота вільних незатухаючих коливань тієї ж коливальної системи, тобто при d = 0 (при відсутності втрат енергії).

Рішення рівняння у випадку малих згасань ()

,

де - амплітуда затухаючих коливань, а – початкова амплітуда.

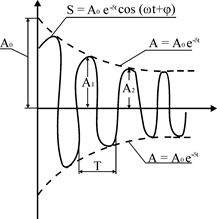
Рис.

Проміжок часу , за який час амплітуда затухаючих коливань зменшується в е разів, зветься часом релаксації.

Якщо затухання мале, то можна умовно користуватись поняттям періоду як проміжок часу між двома послідовними максимумами (чи мінімумами) коливальної фізичної величини. Тоді період затухаючих коливань з урахуванням формули

рівняється .

Якщо A(t) і A(t+T) - амплітуди двох послідовних коливань, відповідних моментам часу, що відрізняються на період, то відношення

називається декрементом затухання, а його логарифм

- логарифмічним декрементом затухання;

N – число коливань, здійснюваних за час зменшення амплітуди у е разів.

Для характеристики коливальної системи користуються поняттям добротності Q яка при малих значенням логарифмічного декремента дорівнює

, а поскільки згасання невелике () то Т прийнято рівним .

Застосуємо висновки, одержані для вільних затухаючих коливань лінійних систем, для коливань різної фізичної природи, для пружинного маятника масою m , що здійснює малі коливання під дією пружної сили F = -кх , сила тертя пропорційна швидкості, тобто , де r – коефіцієнт опору; знак мінус указує на протилежні напрямки тертя і швидкості.

За даних умов закон руху маятника матеме вигляд:

Використовуючи формулу і вважаючи, що коефіцієнт затухання , одержимо диференціальне рівняння затухаючих коливань маятника:

Маятник коливається по закону з частотою .