Учебное пособие: Експериментальна аерогідродинаміка та гідравліка

Рис.8. Втрати напору на тертя

Але квадратична залежність Дарсі-Вейсбаха виявилася дуже зручною для практики і доцільною з погляду одноманітності розрахунків. Цією формулою користуються при обчисленнях як ламінарних, так і турбулентних режимів руху. А відхилення від квадратичної залежності враховується тим, що значення коефіцієнта l ставиться у пряму залежність від Re, шорсткості поверхні D тощо. Визначенню впливу різних факторів на l присвячено багато експериментальних робіт.

Найбільш цінними своєю систематичністю та широким діапазоном досліджень є експерименти, які виконав Нікурадзе. На рис.9 наведено графік, побудований за даними Нікурадзе. Як видно з графіка, залежність l=f (Re,D) є дуже складною.

Для з’ясування фізичної суті цієї закономірності розглянемо структуру потоку рідини в трубі і шорсткість стінок труби. Абсолютною шорсткістю

К прийнято називати величину виступів, зазубрин, нерівностей на стінці. Експерименти показують, що величина втрат напору н_l залежить не тільки від величини К, але й від форми виступів, частоти та порядку їх розташування. Очевидно також, що одна й та ж абсолютна шорсткість у трубах малого діаметра буде більше впливати на потік, ніж у трубах великого діаметра. А тому більш характерною є величина відносної шорсткості

,

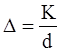де d - діаметр труби.

Присутність твердої поверхні суттєво зменшує величину поперечної пульсації швидкості в пристінному шарі. Експеримент свідчить, що навіть при великих швидкостях потоку, рідина біля стінки труби рухається повільно, упорядковано, обтікаючи виступи та нерівності поверхні. Установлено, що біля стінки реалізується ламінарний режим руху. Товщина ламінарного пристінного прошарку залежить від числа Re та діаметра d:

.

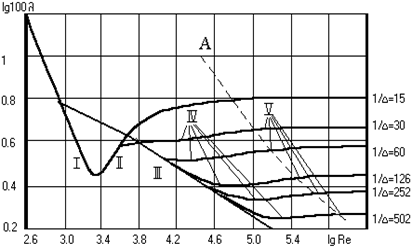
Рис.9. Залежність l від числа Re згідно з результатами дослідів Нікурадзе

У тому разі, коли d>K, тобто коли ламінарний прошарок покриває виступи та нерівності труби, очевидно, що величина шорсткості не буде впливати на втрати напору, і така труба буде гідравлічно гладкою трубою. При d<K вона гідравлічно шорстка. Оскільки d залежить від Re_, то одна й та ж труба може бути гідравлічно гладкою й гідравлічно шорсткою залежно від величини числа Re. Область залежності l=f (Re,D) можна розділити на п’ять характерних зон (рис.9): І - зона ламінарного руху, 0<Re<2320, втрати напору не залежать від шорсткості:

;

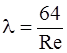ІІ - зона перехідного режиму, 2320<Re<4000, втрати також не залежать від шорсткості поверхні:

,

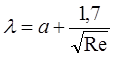де a»0,02 для водопровідних труб із середньою шорсткістю; ІІІ - зона гідравлічно гладких труб, 4000<Rе<40, шорсткість не впливає на втрати напору:

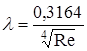(формула Блазiуса);

ІV - зона шорстких труб, 40<Rе<500, втрати напору залежать і від числа Re і від шорсткості:

(формула Альтшуля);

V - зона квадратичного опору (або зона автомодельності), Rе>500, втрати напору залежать тільки від шорсткості:

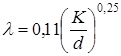(формула Шифринсона).

Необхідно зазначити, що для ІІ-V зон відомо багато інших емпіричних формул, за якими визначають коєфіцієнт l.

1.4.1 Лабораторна работа. Визначення коефіцієнта опору тертя

МЕТА РОБОТИ:

1. Для різних значень чисел Re визначити експериментально величину коефіцієнта опору тертя трубопроводу l_Д .

2. За результатами досліду визначити величину шорсткості труби К.

3. Обчислити величину коефіцієнта l_Ф за формулами й порівняти зі значеннями коефіцієнтів l_Д , одержаними експериментально.

4. Побудувати графіки залежностей

та .