Учебное пособие: Інваріантні підпростори. Власні вектори і власні значення лінійного оператора

Власний вектор є ненульовим розв’язком системи (4´). Як відомо, однорідна система n лінійних рівнянь з n невідомими має ненульові розв’язки тоді і тільки тоді, коли її детермінант дорівнює нулю, тобто, коли виконується умова

Так як детермінант при транспонуванні не змінюється, то одержимо рівняння відносно невідомого

(5)

Отже, ми довели теорему : кожне власне значення лінійного оператора , заданого матрицею А, є коренем характеристичного многочлена.

Провівши міркування знизу вверх, одержимо твердження: кожний корінь характеристичного многочлена лінійного оператора буде його власним значенням.

В ході доведення теореми ми одержали схему знаходження власних значень і власних векторів лінійного оператора.

Приклад. Знайти власні значення і власні вектори лінійного оператора заданого матрицею

Схема розв’язування :

1. Складаємо характеристичну матрицю

.

2. Шукаємо характеристичний многочлен

=

3. Розв’язуємо характеристичне рівняння

(2-

Отже, власними значеннями лінійного оператора є числа 1, 2, -1.

4. Для знаходження власних векторів розв’язуємо систему рівнянь

тобто (5)

а) Шукаємо власні вектори, які відповідають власному значенню підставивши у (5) замість одиницю:

або в розгорнутому вигляді

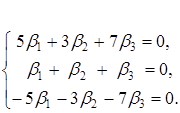
Ранг цієї системи дорівнює 2, тому фундаментальна система її розв’язків складається з одного розв’язку. Знаходимо його. Зліва залишаємо змінні , а перенесемо в праву частину і вважаємо її відомою: 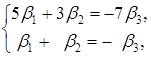звідси Покладемо тоді . Отже, одним із власних векторів, які відповідають власному значенню є вектор Всі власні вектори, які відповідають цьому значенню мають вигляд , де -будь-яке дійсне число, відмінне від нуля.

Самостійно знайти власні вектори, які відповідають власним значенням 2 і .

Весь набір характеристичних коренів оператора (причому кожний корінь береться з тією кратністю, яку він має в характеристичному рівнянні) називається спектром лінійного оператора.

Сукупність власних векторів оператора , яким відповідає одне і те саме власне значення , збігається з сукупністю всіх ненульових розв’язків систем лінійних однорідних рівнянь.

Лінійні оператори з простим спектром