Учебное пособие: Інваріантні підпростори. Власні вектори і власні значення лінійного оператора
Повернемося до питання: чи існує базис простору ![]() , в якому лінійний оператор
, в якому лінійний оператор ![]() задається діагональною матрицею.
задається діагональною матрицею.
Нехай в просторі ![]() існує базис, який складається з власних векторів
існує базис, який складається з власних векторів ![]() , які відповідають власним значенням
, які відповідають власним значенням ![]() , відповідно. Знайдемо матрицю цього оператора в цьому базисі:
, відповідно. Знайдемо матрицю цього оператора в цьому базисі:
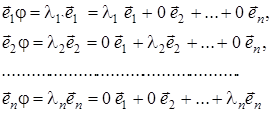
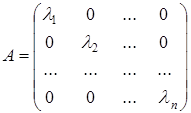
тобто оператор ![]() заданий діагональною матрицею, причому по діагоналі стоять власні значення лінійного оператора, які відповідають власним векторам базису.
заданий діагональною матрицею, причому по діагоналі стоять власні значення лінійного оператора, які відповідають власним векторам базису.
Навпаки. Нехай лінійний оператор ![]() в деякому базисі
в деякому базисі ![]() задається довільною матрицею
задається довільною матрицею 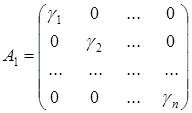 .
.
За означенням матриці лінійного оператора в даному базисі ![]()
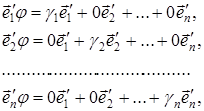 звідси
звідси 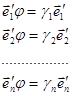 тобто вектори базису
тобто вектори базису![]() є власними векторами оператора
є власними векторами оператора ![]() з власними значеннями
з власними значеннями ![]() . Таким чином ми довели теорему :
. Таким чином ми довели теорему :
Якщо вектори базису ![]() є власними векторами лінійного оператора
є власними векторами лінійного оператора ![]() , то в цьому базисі оператор
, то в цьому базисі оператор ![]() задається діагональною матрицею. Навпаки, якщо в деякому базисі матриця оператора
задається діагональною матрицею. Навпаки, якщо в деякому базисі матриця оператора ![]() є діагональною, то всі вектори цього базису є власними векторами оператора
є діагональною, то всі вектори цього базису є власними векторами оператора ![]() .
.
Як бачимо, матриця оператора ![]() в базисі, що складається з власних векторів цього оператора, має досить простий вигляд. Саме це і обумовлює важливість ролі власних векторів, а, отже, і одновимірних інваріантних підпросторів при вивченні лінійних операторів.
в базисі, що складається з власних векторів цього оператора, має досить простий вигляд. Саме це і обумовлює важливість ролі власних векторів, а, отже, і одновимірних інваріантних підпросторів при вивченні лінійних операторів.
Виникає питання: як встановити, знаючи матрицю оператора ![]() в деякому базисі, чи має цей оператор власні вектори, які утворюють базис простору тобто, чи можна оператор
в деякому базисі, чи має цей оператор власні вектори, які утворюють базис простору тобто, чи можна оператор ![]() задати в деякому базисі діагональною матрицею?
задати в деякому базисі діагональною матрицею?
Теорема . Якщо лінійний оператор ![]() має простий спектр, то існує базис простору
має простий спектр, то існує базис простору ![]() , в якому цей оператор задається діагональною матрицею.
, в якому цей оператор задається діагональною матрицею.
Доведення. Дано: ![]() – різні власні значення оператора
– різні власні значення оператора ![]() , яким відповідають власні вектори
, яким відповідають власні вектори ![]() , відповідно, тобто
, відповідно, тобто ![]() , і=1, 2,…, n .
, і=1, 2,…, n .
Оскільки ![]()
![]() , і
, і ![]() , то
, то ![]() – лінійно незалежні, а значить утворюють базис векторного простору
– лінійно незалежні, а значить утворюють базис векторного простору ![]() . В цьому базисі оператор
. В цьому базисі оператор ![]() задається діагональною матрицею
задається діагональною матрицею
вектор ортогональний інваріантний матриця
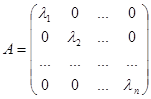 .
.
Теорему доведено.
Зведення матриці до діагонального вигляду
Нехай ![]() квадратна матриця порядку
квадратна матриця порядку ![]() з елементами з поля P .
з елементами з поля P .
Вважають, що матриця A зводиться до діагонального вигляду, якщо існує діагональна матриця, подібна матриці A .
Часто трапляється, що треба знати, чи зводиться квадратна матриця до діагонального вигляду. На основі попередніх результатів можна довести теорему, яка встановлює достатні умови звідності матриці до діагонального вигляду.
Теорема. Кожна квадратна матриця n- го порядку над полем Р , яка має в полі Р n різних характеристичних коренів, зводиться до діагонального вигляду, тобто подібна до діагональної матриці.
Доведення. Дано A – квадратна матриця n – гопорядку над полем P . Нехай ![]() - різні характеристичні корені матриці і
- різні характеристичні корені матриці і ![]() (i=1,2,… n).
(i=1,2,… n).
Розглянемо векторний простір ![]() над полем P . Матриця A в деякому базисі задає деякий лінійний оператор
над полем P . Матриця A в деякому базисі задає деякий лінійний оператор ![]() . Характеристичні корені
. Характеристичні корені ![]() є власними значеннями оператора
є власними значеннями оператора ![]() , яким відповідають власні вектори цього оператора
, яким відповідають власні вектори цього оператора ![]() ,
, ![]() . За властивістю власних векторів, які відповідають різним власним значенням вектори
. За властивістю власних векторів, які відповідають різним власним значенням вектори ![]() – лінійно незалежні, тому вони утворюють базис простору
– лінійно незалежні, тому вони утворюють базис простору ![]() . В цьому базисі матриця лінійного оператора
. В цьому базисі матриця лінійного оператора ![]() має вигляд
має вигляд 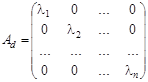 .
.
![]() i A подібні, бо вони задають один і той самий оператор
i A подібні, бо вони задають один і той самий оператор ![]() в різних базисах. Діагональними елементами матриці
в різних базисах. Діагональними елементами матриці ![]() є характеристично корені матриці A.
є характеристично корені матриці A.
Знаходження діагональної матриці, подібної матриці A , називається зведенням матриці A до діагонального вигляду.
Приклад. Звести квадратну матрицю A до діагонального вигляду, якщо
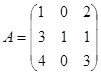 .
.
Розв’язуємо характеристичне рівняння: 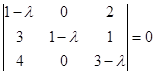
![]() ,
, ![]() . (Розв’язати самостійно)
. (Розв’язати самостійно)