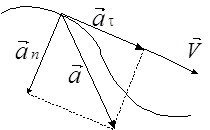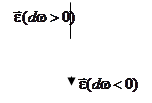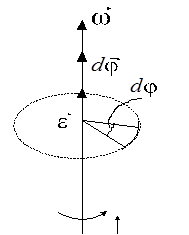Учебное пособие: Механика, молекулярная физика и термодинамика
Основная задача кинематики заключается в нахождении закона движения материальной точки. Для этого используются следующие соотношения:
; 
; 
; 
;
.
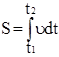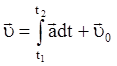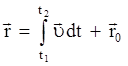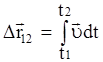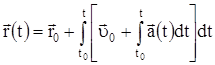Частные случаи прямолинейного движения:
1) равномерное прямолинейное движение: 
;
2) равноускоренное движение: 
.
1.3. Тангенциальная и нормальная составляющие ускорения
Часто используется представление ускорения через две составляющие: тангенциальное и нормальное ускорения (рис. 2):
|
Рис. 2 |
|
;
.Тангенциальное ускорение характеризует быстроту изменения скорости по модулю (величине) и направлено по касательной к траектории:
,
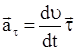где 
- производная модуля скорости; 
- единичный вектор касательной, совпадающий по направлению со скоростью 
.
Нормальное ускорение характеризует быстроту изменения скорости по направлению и направлено по нормали к траектории, к центру кривизны траектории в данной точке:
,
где R - радиус кривизны траектории, 
- единичный вектор нормали.
В случае, если известны модули составляющих векторов, модуль вектора ускорения может быть найден по формуле
.
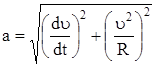1.4. Вращательное движение и его кинематические характеристики
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для характеристики вращательного движения вводятся следующие кинематические характеристики (рис. 3).
Угловое перемещение 
- вектор, численно равный углу поворота тела 
за время
и направленный вдоль оси вращения так, что если смотреть вдоль него, то поворот тела наблюдается происходящим по часовой стрелке.
|
|
Угловая скорость 
- характеризует быстроту и направление вращения тела. Она равна производной угла поворота по времени и направлена вдоль оси вращения как угловое перемещение.
При вращательном движении справедливы следующие формулы:
; 
; 
.
Угловое ускорение 
характеризует быстроту изменения угловой скорости с течением времени, равно
первой производной угловой скорости и направлено вдоль
оси вращения:
; 
; 
.
Зависимость 
выражает закон вращения тела.
При равномерном вращении e = 0, w = const, j = wt.
При равнопеременном вращении e = const, 
, 
.
Для характеристики равномерного вращательного движения используют период вращения и частоту вращения.