Учебное пособие: Механика, молекулярная физика и термодинамика

Частота вращения n - количество оборотов, совершаемых телом за единицу времени. Угловую скорость можно выразить через частоту:

.

Связь между угловыми и линейными кинематическими характеристиками (рис. 4):

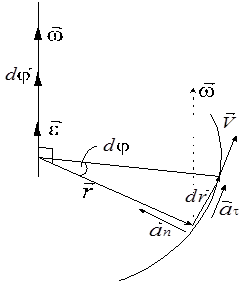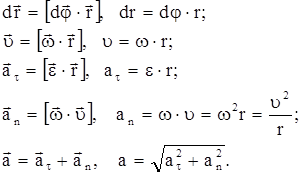
2. Динамика поступательного и вращательного движения.

2.1. Законы Ньютона

Первый закон Ньютона : Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния.

Тела, не подверженные внешним воздействиям, называются свободными телами. Первый закон будет выполняться только в инерциальных системах отсчёта (ИСО). ИСО - система отсчёта, связанная со свободным телом, по отношению к ней любое свободное тело будет двигаться равномерно и прямолинейно или находиться в состоянии покоя. Из относительности движения следует, что система отсчёта, движущаяся равномерно и прямолинейно по отношению к ИСО, также является ИСО. ИСО играют важную роль во всех разделах физики. Это связано с принципом относительности Эйнштейна, согласно которому математическая форма любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчёта.

К основным понятиям, используемым в динамике поступательного движения, относятся сила, масса тела, импульс тела (системы тел).

Силой называется векторная физическая величина, являющаяся мерой механического действия одного тела на другое. Механическое действие возникает как при непосредственном контакте взаимодействующих тел (трение, реакция опоры, вес и т.д.), так и посредством силового поля , существующего в пространстве (сила тяжести, кулоновские силы и т.д.). Сила характеризуется модулем, направлением и точкой приложения.

Одновременное действие на тело нескольких сил ,,..., может быть заменено действием результирующей (равнодействующей) силы :

=++...+=.

Массой тела называется скалярная величина, являющаяся мерой инертности тела. Под инертностью понимается свойство материальных тел сохранять свою скорость неизменной в отсутствии внешних воздействий и изменять её постепенно (т.е. с конечным ускорением) под действием силы. Массы всех тел определяются по отношению к массе тела, принятого за эталон.

Импульсом тела (материальной точки) называется векторная физическая величина, равная произведению массы тела на его скорость: .

Импульс системы материальных точек равен векторной сумме импульсов точек, составляющих систему: .

Второй закон Ньютона : скорость изменения импульса тела равна действующей на него силе:

.

В частном случае (при постоянной массе): ускорение, приобретаемое телом относительно инер­ци­аль­ной системы отсчета, прямо пропорционально действующей на него силе и обратно пропорционально массе тела:

.

Третий закон Ньютона : Силы, с которыми действуют друг на друга взаимо­дей­ствующие тела, равны по величине и противоположны по направлению.

,

где - сила, действующая на 1-ую точку со стороны 2-ой,

- сила, действующая на 2-ую точку со стороны 1-ой.

Из третьего закона следует, что в любой механической системе материальных то­чек геометрическая сумма всех внутренних сил (т.е. сил, с которыми взаимо­действуют между собой материальные точки системы) равна нулю.

2.2. Динамика вращательного движения твердого тела.

Вращательное действие силы харак­те­ризуется такой величиной, как мо­мент силы относительно оси вращения (рис. 5).

Пусть М - точка приложения силы , - радиус-вектор точки М, проведённый пер­пен­дикулярно оси вращения O'O. Разложим на три составляющие:

- осевая, параллельная оси вращения,

- радиальная, направленная вдоль вектора ,

- касательная, перпендикулярная и оси вращения.

Составляющие и - вращения тела вокруг оси O'O не создают. Вращающее действие силы создаётся составляющей . Моментом силы относительно оси вращения O'O называется векторное произведение радиуса-вектора точки приложения силы, проведённого перпен­дикулярно оси вращения, на составляющую силы , перпендикулярную оси вращения и радиусу вектору :

.

Вектор момента силы направлен вдоль оси вращения и связан с направлением силы правилом правого винта.

Если на тело действует несколько сил, то результирующий момент сил равен векторной сумме моментов всех сил, действующих на тело.

Момент инерции тела характеризует инертные свойства тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.

- момент инерции материальной точки массой m, находящейся на расстоянии r от оси.

- момент инерции системы материальных точек.

- момент инерции тела, где - плотность тела.

Момент инерции тела относительно произвольной оси может быть рассчитан по

теореме Штейнера : момент инерции тела