Учебное пособие: Непрерывность функции на интервале и на отрезке

Точно так же далее доказывается, что при всех , при всех , ит.д. Итак, - возрастающая последовательность, ограниченная сверху числом . Поэтому существует . Из непрерывности функции следует, что существует , но при , так что предела не существует. Полученное противоречие доказывает, что функция ограничена сверху.

Аналогично доказывается, что ограничена снизу, откуда следует утверждение теоремы.

Очевидно, что ослабить условия теоремы нельзя: если функция не является непрерывной, то она не обязана быть ограниченной на отрезке (приведём в качестве примера функцию

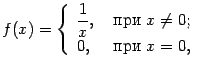
на отрезке . Эта функция не ограничена на отрезке, так как при имеет точку разрыва второго рода, такую что при . Также нельзя заменить в условии теоремы отрезок интервалом или полуинтервалом: в качестве примера рассмотрим ту же функцию на полуинтервале . Функция непрерывна на этом полуинтервале, но неограничена, вследствие того что при .

Поиск наилучших постоянных, которыми можно ограничить функцию сверху и снизу на заданном отрезке, естественным образом приводит нас к задаче об отыскании минимума и максимума непрерывной функции на этом отрезке. Возможность решения этой задачи описывается следующей теоремой.

Теорема 3.9 (о достижении экстремума непрерывной функцией) Пусть функция непрерывна на отрезке . Тогда существует точка , такая что при всех (то есть - точка минимума: ), и существует точка , такая что при всех (то есть - точка максимума: ). Иными словами, минимальное и максимальное⁸ значения непрерывной функции на отрезке существуют и достигаются в некоторых точках и этого отрезка.

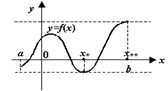
Рис.3.24. Непрерывная на отрезке функция достигает максимума и минимума

Доказательство. Так как по предыдущей теореме функция ограничена на сверху, то существует точная верхняя грань значений функции на - число . Тем самым, множества , ,..., ,..., не пусты, и по предыдущей лемме в них есть наименьшие значения : , . Эти не убывают (доказывается это утверждение точно так же, как в предыдущей теореме):

и ограничены сверху числом . Поэтому, по теореме о пределе монотонной ограниченной последовательности, существует предел Так как , то и

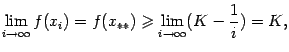
по теореме о переходе к пределу в неравенстве, то есть . Но при всех , и в том числе . Отсюда получается, что , то есть максимум функции достигается в точке .

Аналогично доказывается существование точки минимума.

В этой теореме, как и в предыдущей, нельзя ослабить условия: если функция не является непрерывной, то она может не достигать своего максимального или минимального значения на отрезке, даже будучи ограниченной. Для примера возьмём функцию

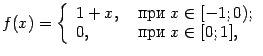
на отрезке . Эта функция ограничена на отрезке (очевидно, что ) и , однако значение1 она не принимает ни в одной точке отрезка (заметим, что , а не 1). Дело в том, что эта функция имеет разрыв первого рода в точке , так что при предел не равен значению функции в точке0. Далее, непрерывная функция, заданная на интервале или другом множестве, не являющемся замкнутым отрезком (на полуинтервале, полуоси) также может не принимать экстремального значения. В качестве примера рассмотрим функцию на интервале . Очевидно, что функция непрерывна и что и , однако ни значения0, ни значения1 функция не принимает ни в какой точке интервала . Рассмотрим также функцию на полуоси . Эта функция непрерывна на , возрастает, принимает своё минимальное значение0 в точке , но не принимает ни в какой точке максимального значения (хотя ограничена сверху числом и