Учебное пособие: Операционный менеджмент
Сглаживая тренд, уравнение для коррекции тренда использует константу сглаживания , так же как в простой экспоненциальной модели использовалась
Т t рассчитывается с помощью равенства
T t = ( 1 – ) T t-1 + ( F t - F t-1 ) (4.7)
где T t — сглаженный тренд для периода t ,
Т t-1 — сглаженный тренд для предыдущего периода;
— константа сглаживания, которую мы выбираем;
F t — прогноз простого экспоненциального сглаживания для периода t ,
F t-1 — прогноз для предыдущего периода.
Имеются три шага расчета прогноза с регулируемым трендом.
Шаг 1. Расчет простого экспоненциального прогноза для периода t (Ft )
Шаг 2. Расчет тренда с использованием уравнения T t = ( 1- ) T t-1 + (F t – F t-1 )
Для начала шага 2 для первого периода начальное значение тренда должно быть заложено (или как хорошее предположение, или как обзор прошлых данных). После этого рассчитывается тренд.
Шаг 3. Расчет прогноза с регулируемым трендом методом экспоненциального сглаживания по формуле FIT t = F t + T t
5. Трендовое проектирование. Метод прогнозирования на основе прошлых временных серий, который мы будем обсуждать, называется трендовым проектированием. Этот метод устанавливает линию тренда по серии точек прошлых данных, а затем проектирует линию в будущее для средне- и долгосрочных прогнозов. Ряд математических уравнений-трендов может быть использован (на пример, экспоненциальные и квадратные), но в данной секции мы будем рассматривать только линейные (прямолинейные) тренды.
Если мы решили развивать линейный тренд линейно точным статистическим методом, то можем применить метод наименьших квадратов. Этот метод позволяет получить прямую линию, которая минимизирует сумму квадратов вертикальных разностей между линией и каждым текущим наблюдением.
Линия, полученная методом наименьших квадратов, описывается в терминах ее значения (высотой, отсекаемой ею на оси у) и ее наклоном (линейным углом). Если мы можем рассчитать отсекаемое значение и наклон, то можем описать линию следующим уравнением:
у = а + bх, (4.8)
где у — расчетное значение предсказываемой переменной (зависимой переменной);
а — отрезок, отсекаемый прямой на оси у;
b — наклон линии регрессии (или коэффициент изменения значения у по отношению к изменению значения х);
х — независимая переменная (в данном случае время).
Статистически, имея уравнение, мы можем найти значения а и b для некоторой линии регрессии. Наклон линии регрессии находим так:
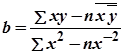 (4.9)
(4.9)
где b— наклон линии регрессии;
![]() — сумма значений;
— сумма значений;
х— значения независимой переменной;
у — значения зависимой переменной;
![]() — среднее значение х;
— среднее значение х;
![]() — среднее значение у,
— среднее значение у,