Учебное пособие: Основные правила дифференцирования

Имеем Δy≈dy=f'(x)·Δx.

f'(x)=2x – 2 ,f'(3)=4, Δx=0,01.

Поэтому Δy ≈ 4·0,01 = 0,04.

2. Вычислить приближенно значение функции в точке x = 17.

Пусть x₀ = 16.

Тогда Δx = x – x₀ = 17 – 16 = 1,

,

.

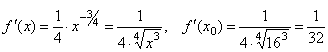Таким образом, .

3. Вычислить ln 0,99.

Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.

Положим x₀ = 1. Тогда Δx = – 0,01, f(x₀ )=0.

, f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.