Учебное пособие: Переходные процессы в колебательных контурах

Он получается при .

Для построения графика (рис. 7) используем выражение:

,

где – амплитуда напряжения, убывающая по экспоненциальному закону.

Рис. 7

Длительность переходных колебаний может быть найдена из условия, что амплитуда напряжения будет менее 5% от своего максимального значения, т. е.:

, откуда .

Отсюда можно сделать вывод, что чем выше добротность контура (или чем меньше полоса пропускания ), тем более длительным будет переходный процесс.

Частота затухающих колебаний , однако это отличие незначительно. Действительно при средней добротности (), например , имеем: .

в) Критический режим.

Он возникает, когда .

В этом случае и получается неопределенность .

Раскроем ее:

.

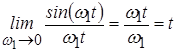Выражение для принимает вид:

.

График этой функции начинается и заканчивается нулем, не пересекает ось времени. Исследуем его на экстремум:

.

Экстремальные точки найдем из условия:

,

при этом:

.

График напряжения в рассматриваемом режиме показан на рисунке 8.

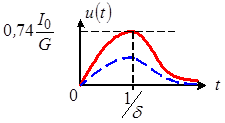
Рис. 8

г) Апериодический режим.

Такой режим получается при (), откуда следует, что будет комплексной и не имеет физического смысла. График напряжения при этом будет менее выраженным, чем при критическом режиме (пунктир на рисунке 8).

Вывод: изменяя добротность контура (например, с помощью шунтирующего сопротивления) можно изменять длительность и вид колебательного процесса.