Учебное пособие: Переходные процессы в колебательных контурах

Переходные колебания в параллельном контуре при гармоническом воздействии

Пусть на параллельный контур с резонансной частотой (рис. 9,а) находящийся при нулевых начальных условиях, в момент действует гармоническое колебание, частота которого совпадает с :

.

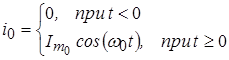Требуется определить закон изменения напряжения на контуре.

Задачу решим в операторной форме, для чего перейдем к схеме замещения, показанной на рисунке 9,б.

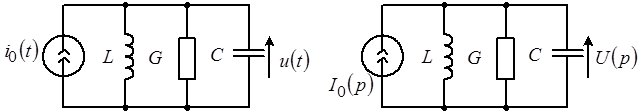
а) б)

Рис. 9

По таблице соответствий воздействие имеет изображение:

.

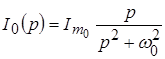Определим операторную проводимость контура:

,

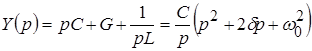где и определены ранее.

По закону Ома в операторной форме имеем:

.

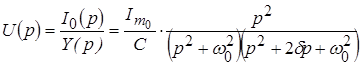Поскольку в таблице соответствий нет нужной формулы для перехода во временную область, то данное выражение следует преобразовать.

Для этого воспользуемся теоремой разложения и методом неопределенных коэффициентов. Представим правильную дробь 4‑го порядка в виде суммы двух правильных дробей 2‑го порядка:

,

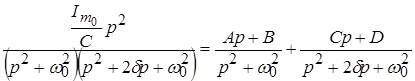где , , , — коэффициенты, подлежащие определению.

Если данное выражение привести к общему знаменателю, раскрыть скобки в числителе и приравнять коэффициенты при одинаковых степенях , то получим систему 4‑х уравнений с 4‑мя неизвестными.

Решая систему уравнений имеем: ; ; .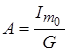

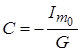Теперь полученное выражение можно записать в виде:

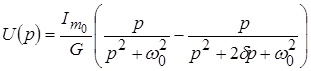
и использовать таблицу соответствий.

По таблице соответствий находим оригинал:

.

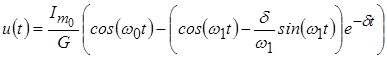Предполагая, что контур имеет добротность, при которой , 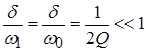и, пренебрегая произведением 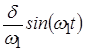как очень малой величиной, получим:

.

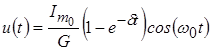Из формулы следует, что процесс установления гармонического напряжения в контуре до амплитудного значения происходит не мгновенно, а за конечное время, определяемое множителем .