Учебное пособие: Проектирование и разработка нефтяных и газовых месторождений

находят распределение давления по глубине.

При известном давлении на устье Ру формула имеет следующий вид:

,

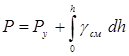где h – глубина скважины.

При известном забойном давлении Рз

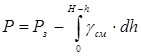
где Н – глубина скважины.

При определении расходного газосодержания следует учитывать как свободный газ, поступающий в скважину из пласта, или газ, закачиваемый в скважину при газлифтном способе эксплуатации, так и газ, выделяющийся из нефти при подъеме жидкости вверх. Обозначим массовый дебит свободного газа через qгс. Примем линейный закон растворимости газа в нефти (закон Генри) и рассмотрим участок подъемника длиной dh. Изменение qг на этом участке происходит за счет выделения газа из нефти, т. е. баланс массы газа за время dt будет:

где а – коэффициент Генри; ρго – плотность газа при нормальных условиях; F – площадь поперечного сечения труб.

Δq2 = q2 (h + dh) – q (h)

Δp = p (h) – p (h + dh)

Учтем, что dh = υж · dt, тогда получим:

где υж – скорость движения жидкости в трубах.

Расходное газосодержание

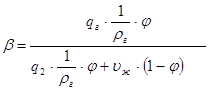
Очевидно, что υж · (1 - φ) · F = Q,

где Q – дебит скважины

Зная зависимость φ = φ (β) находим распределение давления по стволу скважины Р, объемное газосодержание φ и дебит газа qг.

Теперь рассмотрим особенности расчета подъемника высоковязкой жидкости. В этом случае необходимо учесть потери давления на трение, т.е.:

где - скорость движения смеси;

λсм – коэффициент гидравлического сопротивления смеси.

λсм можно оценить по формуле λсм ≈ λж; при ламинарном движении потока . При высокой вязкости откачиваемой жидкости необходимо учитывать изменение температуры потока по глубине, т.к. вязкость очень сильно зависит от температуры. Распределение температуры по глубине можно определить опытным путем или расчетным.

Рассмотрим установившийся поток в подъемных трубах. По мере подъема жидкости температура ее понижается в результате теплообмена с окружающей средой. Получим уравнение теплового баланса.

Пусть в сечении h температура потока равна T(h), соответственно в сечении h + Δh – T (h + Δh). Время, за которое жидкость проходит расстояние Δh, равно , где u – скорость движения потока. Обозначим через с – теплоемкость системы, то изменение количества тепла в элементе (h; h + Δh) за время Δt будет равно: