Учебное пособие: Расчет основных статистических характеристик и взаимосвязь результатов измерений
Таблица 2.
| Хi | Уi | Хi – | (Хi–)2 | Уi– | (Уi–)2 | (Хi–)(Уi–) |
| 10,2 | 25,0 | – 0,87 | 0,76 | –5,1 | 26,01 | 4,44 |
| 10,3 | 28,3 | – 0,77 | 0,59 | –1,8 | 3,24 | 1,39 |
| 10,5 | 28,0 | – 0,57 | 0,33 | –2,1 | 4,41 | 1,2 |
| 11,0 | 29,0 | –0,07 | 0,005 | –1,1 | 1,21 | 0,08 |
| 11,2 | 32,1 | 0,13 | 0,02 | 2,0 | 4 | 0,26 |
| 11,8 | 33,0 | 0,73 | 0,53 | 2,9 | 8,41 | 2,12 |
| 12,0 | 33,0 | 0,93 | 0,86 | 2,9 | 8,41 | 2,7 |
| 11,5 | 33,2 | 0,43 | 0,18 | 3,1 | 9,61 | 1,33 |
| 10,9 | 29,9 | –0,17 | 0,03 | –0,2 | 0,04 | 0,034 |
| 11,3 | 29,8 | 0,23 | 0,05 | –0,3 | 0,09 | –0,0690 |
| ∑ =110,7 ∑=301,3 ∑ = 3,355 | ∑=65,43 ∑ = 13,485 | |||||
Коэффициент корреляции rху = 0,91 указывает на то, что у исследуемых 10 игроков связь между силой броска и дальностью полета мяча линейная, положительная и сильная.
Оценим статистическую достоверность коэффициента корреляции, т.е. сравним полученное (наблюдаемое) значение коэффициента корреляции с табличным (Приложение, табл. 2).
Но : r ген. = 0, Н1 : r ген. > 0
Находим по таблице для n =10 и α = 0,05 критическое значение коэффициента корреляции
r крит. = 0,549
Вывод: Так, как r набл. (0,91) > r крит. (0,549), принимается конкурирующая гипотеза о статистической достоверности коэффициента корреляции с вероятностью более 0,95. Поэтому можно считать, что между силой броска и дальностью полета мяча существует сильная линейная корреляционная связь не только в нашей выборке (10 гандболистов), но и во всей генеральной совокупности.
Чтобы рассчитать процент зависимости дальности полета мяча от силы броска, определим коэффициент детерминации по формуле:
Д = r ху2 *100%
Д = 0,912 * 100% = 82,81%
Вывод: Разброс результатов дальности полета мяча на 82,81% объясняется величиной силы броска и на 100% – 82,81% = 17,19% – другими причинами.
6. Построение гистограммы . Так как исследуется выборка малого объема 10,20; 10,30; 10,50; 11,0; 11,2; 11,8; 12,0; 11,5; 10,9; 11,3, выбираем число интервалов К=4.
На основании полученных значений составим таблицу, в которой столбец 1 представляет номера интервалов, столбец 2 границы интервалов, которые получают с установленным шагом, в столбце 3 фиксируют частоту или встречаемость значения выборки в каждом интервале.
| № интервала | границы интервала | частота |
| 1 | 2 | 3 |
| 1 | 10,2 – 10,65 | 3 |
| 2 | 10,65 – 11,1 | 2 |
| 3 | 11,1 – 11,55 | 3 |
| 4 | 11,55 – 12,0 | 2 |
Построим диаграмму из смежных прямоугольников (гистограмму). Основания этих прямоугольников равны интервалам; в целях облегчения построения гистограммы высоты прямоугольников примем равными соответствующим частотам.
Рис.2 Гистограмма (по абсциссе – середины интервалов, по ординате – частоты)
 |
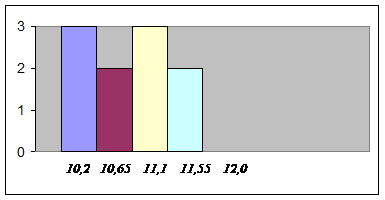7. Требования к оформлению работы .
Контрольную работу выполните в отдельной тетради, аккуратно, без помарок. На обложке тетради напишите:
Контрольная работа по спортивной метрологии
Студента …….. группы …курса … факультета …заочной формы обучения
Фамилия, И.О.
На 1-ой странице в правом углу укажите номер варианта задания, полученного на кафедре биомеханики, а в середине страницы – тема работы и само задание.
Перед выполнением соответствующего подраздела задания перепишите и подчеркните его номер и название.
Ответы на теоретические вопросы должны быть не очень многословными, но достаточно полно характеризовать сущность вопросов.
В формулах, приводимых в теоретических сведениях, должны быть указаны названия (определения) всех входящих в них величин.
После выполнения расчетов должны быть указаны размерности рассчитанных величин (см, кг, с, % и т.д.).
В случае невыполнения требований к оформлению работа возвращается без проверки.
ЛИТЕРАТУРА
1. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск,1984.
2. Начинская С.В. Основы спортивной статистики. – Киев, 1987.
3. Основы математической статистики: Учебное пособие для институтов физической культуры. – М., ФиС, 1990.