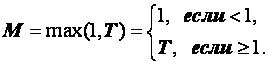Учебное пособие: Разностные схемы для уравнений параболического типа

Из формул (3.15), (3.16) следует, что разностные схемы (3.13), (3.14) аппроксимируют задачу с погрешностью порядка S относительно h .

Разностная схема (3.13) позволяет по значениям решения на нулевом слое, то есть по значениям вычислить значения на первом слое . Для этого достаточно в (3.13) положить n = 0и произвести вычисления, носящие рекурсионный характер. Потом по значениям можно аналогично при n = 1 вычислить значения и т.д. В силу этого разностную схему (3.13) называют явной .

Разностная схема (3.14) такими свойствами не обладает. Действительно, если мы в (3.14) положим n = 0, то в левой части полученной формулы будет линейная комбинация из значений , в правой части будут значения известной функции и . Для вычисления значений на первом слое в этом случае необходимо решать бесконечную систему линейных уравнений. По этой причине схему (3.14) называют неявной .

2. Устойчивость двухслойных разностных схем

Определим норму в пространстве по правилу

.

Рассмотрим явную разностную схему (3.13). Выясним, при каких значениях r , возможна устойчивость этой схемы.

Для доказательства устойчивости надо показать, что разностная схема однозначно разрешима и при любых

,

имеет место оценка ,

гдеМ – постоянная, не зависящая от и и .

Разностная схема (3.13) – явная, и поэтому ее однозначная разрешимость очевидна.

Перепишем формулу в виде

, , (3.17)

.

Пусть выполнено условие

или 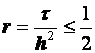. (3.18)

Тогда из (3.17) получим:

,

или

. (3.19)

Неравенство (3.19) означает, что при , не превосходит ,тоесть невозрастает с увеличением n .

Это свойство однородной разностной схемы принято называтьпринципом максимума . Положим в (3.19) . Это даст

,

,

.

Заметим, что есть число, независящее от m и n . Просуммировав последние неравенства и, учитывая, что , получим

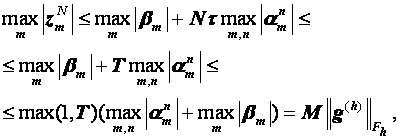(3.20)

где обозначено