Учебное пособие: Разностные схемы для уравнений параболического типа

Рассмотрим задачу Коши для уравнения теплопроводности

, , , (3.5)

с условием на прямойt = 0

, . (3.6)

Требуется найти функцию , которая при и удовлетворяла бы уравнению (3.5), а при выполняла бы условие (3.6).

Будем считать, что задача (3.5), (3.6) имеет в верхней полуплоскости единственное решение , непрерывное вместе со своими производными

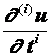, i = 1, 2 и 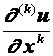, k = 1, 2, 3, 4.

Запишем задачу (3.5), (3.6) в виде . Для этого достаточно положить

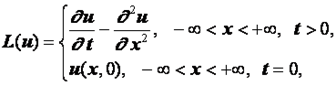
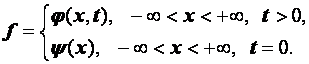
Будем далее считать, что t изменяется в пределах . В рассматриваемом случае

,

Г − объединение прямыхt= 0иt=T .

Выберем прямоугольную сетку и заменим область сеточной областью . К области отнесем совокупность узлов , где

, , ,

, , , .

Заменим задачу разностной схемой вида . Обозначим через точное значение решения задачи в узле , а через – соответствующее приближенное решение. Имеем

Для замены выражений и воспользуемся формулами численного дифференцирования. Имеем:

, (3.7)

, (3.8)

, (3.9)

(3.10)

Назовем некоторую совокупность узлов, привлекаемых для замены задачи в узле , разностной схемой ,шаблоном . Наиболее употребительные шаблоны изображены на рис. 3:

Рис. 3. Явный и неявный шаблоны

Рассмотрим явный двухслойный шаблон. Для него

--> ЧИТАТЬ ПОЛНОСТЬЮ <--