Учебное пособие: Разностные схемы для уравнений параболического типа

или .

Таким образом, разностная схема (3.13) при выполнении условия (3.18), налагаемого на и h , устойчива. Условие (3.18) весьма жестко, ибо из него следует, что

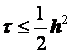. (3.21)

Это приводит к тому, что если мы желаем сохранить устойчивость, то при вычислениях по схеме (3.13) шаг по времени приходится выбирать очень малым.

Обратимся теперь к разностной схеме (3.14), соответствующей шаблону, изображенному на рис. 4,

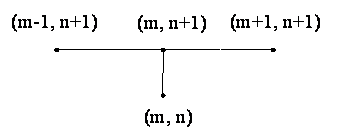
Рис. 4. Неявный двухслойный шаблон

и перепишем ее в виде

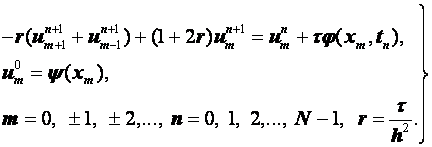(3.22)

Посмотрим, какие надо проделать вычисления, чтобы, используя формулы (3.22), можно было вычислить, например, значения на первом временном слое со значениями на нулевом временном слое. Положив в формулах (3.22) n = 0 , получим:

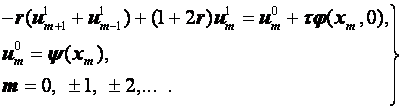(3.23)

Формулы (3.23) представляют собой бесконечную систему линейных уравнений относительно неизвестных .

Решение таких систем является сложной и трудоемкой задачей, поэтому разностные схемы (3.14) неудобны для задач Коши на бесконечных отрезках и применяется редко. Однако если отрезок оси x , на котором рассматривается задача Коши, конечен, то есть , а на прямых x = a и x = b дополнительно заданы некоторые ограничения на решение , то разностные схемы вида (3.14) оказываются весьма эффективными. В частности, можно показать, что такие схемы являются абсолютно устойчивыми, то есть устойчивыми при любых значениях .

Если, например, на отрезках прямых x = a и x = b , заданы условия , , то вид системы (3.23) существенно изменится:

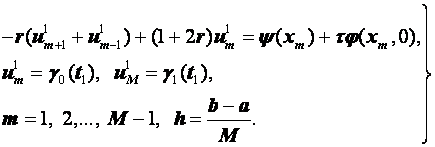(3.24)

Формулы (3.24) представляют собой систему M + 1 алгебраических уравнений относительно . Матрица этой системы трехдиагональна и ее можно решить методом прогонки. Отсюда ясно, что реализация неявных разностных схем требует больших вычислительных затрат для вычисления решения на одном временном слое, но таких слоев может быть немного из-за того, что в этом случае отсутствуют ограничения на соотношение . Если пользоваться явной разностной схемой, то вычисление решения на следующем слое осуществляется по рекурсионному правилу и связано с минимальными вычислительными затратами, однако из-за ограничения

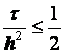
число временных слоев в случае явных схем может быть существенно большим по сравнению с числом временных слоев для неявных схем.

Рассмотрим теперь вопрос о сходимости схемы (3.13). Эта схема аппроксимирует задачу (3.5), (3.6) с погрешностью порядка и устойчива при . Поэтому схема (3.13), по теореме об аппроксимации и устойчивости, будет сходящейся. При этом погрешность для приближенного решения будет величиной порядка .