Учебное пособие: Системи документального електрозв’язку

Лекція 1. Корегуючі коди. Класифікація. Параметри. Згортувальні коди.

Корегуючі коди – це такі коди, в які формуються на основі інформаційної послідовності символів а₁ ,а₂ ... а_к послідовність перевірочних символів в₁ , в₂ ... в_r . в кодері. За допомогою введеної збитковості декодер має можливість в залежності від вибраного коду і алгоритму декодування, виявляти чи виправляти помилково прийняті інформаційні символи, які створені в результаті дії різного роду перешкод в каналі зв’язку.

В класифікаційній діаграмі розглянемо тільки ті коди, що знаходять найбільше застосування в системах документального електрозв’язку.

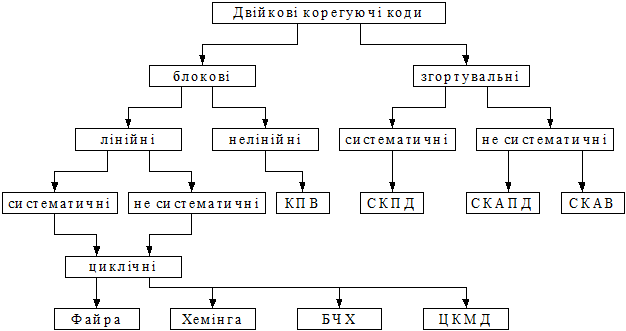
До блокових кодів відносяться такі коди, в яких кодування та декодування здійснюється в межах блоку, який складається з визначеного числа кодових символів. Всі блокові коди характеризуються довжиною блока, або значністю кодової комбінації (КК) n кількістю інформаційних символів k . Для цього прийнято позначення (n, k ).

До згортувальних кодів, або ще як їх називають безперервні, рекурсивні чи ланцюгові відносяться такі коди, в яких процеси кодування та декодування мають безперервний характер, без явного виділення границь при формуванні кодового слова.

Блокові коди в свою чергу діляться на лінійні та нелінійні. До лінійних відносяться такі коди, в яких формування блоків, тобто кодування здійснюється з використанням лінійних операцій над інформаційними символами. В іншому випадку корегуючи коди відносяться до нелінійних . Прикладом нелінійного коду є міжнародний семиелементний код МТА-3,або код с постійною вагою (КПВ). Кожна комбінація такого коду має три одиниці і чотири нуля при всіх можливих варіаціях.

Для лінійних (n, k ) кодів відносяться такі коди, в яких r = n- k збиткових символів формується із k інформаційних за допомогою лінійних операцій, тобто операцій додавання та переключення.

Для двійкових кодів додавання виконується по mod2, тобто 0+1=1, 1+0=1, 0+0=0 і 1+1≡0, а перемноження здійснюється в звичайному порядку.

Перевірочні символи для лінійного групового коду визначається

mod2 j=1, 2,…, r

при цьому необхідно, щоб базові коефіцієнти створювали прямокутну матрицю:

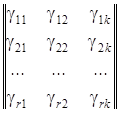, базисні сторони якої лінійно незалежні вектори – строки називаються лінійно незалежними, якщо ні одна з них не може бути представлена в виді лінійної комбінації других, другими словами їх сума не повинна створювати нульову строку .

Лінійні блокові коди мають властивість замкнутості , це означає, що сума по mod2 2-х або більше дозволених КК створює КК, яка належить цьому чи іншому коду. І ще будь-який лінійний код завжди має нульову КК, створену як суму двох однакових КК.

Лінійні коди в свою чергу діляться на систематичні та несистематичні . в систематичних кодах інформаційні символи на виході кодера представлені в явному виді. Належність до систематичних чи до несистематичних кодів визначається вибором коду й алгоритму кодування.

Значну частину лінійних кодів займають циклічні коди, до них відносяться:

– коди Хемінга;

– коди БЧХ (Боуза-Чоудхури-Хоквингема);

– коди з мажоритарним декодуванням (ЦКМД), яким властива проста схемна реалізація декодера;

– коди Файра (виправляють пакети помилково прийнятих кодових символів).

Згортувальні коди як і блокові можна розділити на систематичні та несистематичні . Перші декодуються відносно простим методом – пороговим (ЗКПД), а другі – з використанням алгоритму послідовного декодування (ЗКАПД) і алгоритму Вітербі (ЗКАВ). Несистематичні коди з алгоритмом декодування Вітерці знаходять широке застосування в телекомунікаційному обладнанні.

Параметри. Загальна кількість кодових комбінацій (КК) використовується для передачі тільки повідомлень тільки КК, які називаються дозволеними, решта не використаних КК є забороненими.

Корегуючі коди застосовуються для виявлення або виправлення помилок заданої кратності. Під кратністю помилки розуміють кількість створених символів в КК значністю n. При незалежних помилках в каналі зв’язку ймовірність випадкового виникнення t кратної помилки визначається по формулі Бернуллі:

,

де – біноміальні коефіцієнти;

, якщо , то найбільш вірогідні помилки малої кратності.

Корегуюча здатність двійкових кодів визначається мінімальною кодовою відстанню :

,

де ; j, l = 1, 2,...,2^k ; – номери дозволених КК.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--