Учебное пособие: Статистическое изучение взаимосвязи социально-экономических явлений и процессов

Орел ГТУ, 2003

Чернова А.В., Краснобокая И.А., 2003

Содержание

1. Методические указания по выполнению лабораторной работы

2. Пример выполнения лабораторной работы

2.1 Задание на лабораторную работу

3. Порядок выполнения лабораторной работы

Рекомендуемая литература

Приложение

1. Методические указания по выполнению лабораторной работы

Наиболее разработанной в теории статистики является методология корреляционно-регрессионного анализа парной корреляции, которая исследует связь между одним признаком-фактором (х) и одним признаком-результатом (у).

В основу выявления и установления аналитической формы связи положено применение в анализе исходной информации математических функций, для чего применяют различного вида уравнения прямолинейной и криволинейной связи.

Это уравнение называется уравнением регрессии (или уравнение парной зависимости).

Например, уравнение парной линейной корреляционной зависимости имеет следующий вид:

, (1)

где у_х - теоретические значения результативного признака, полученные по уравнению регрессии;

a₀ , a₁ - коэффициенты (параметры) уравнения регрессии.

Коэффициент парной линейной регрессии а₁ показывает изменение результативного признака у под влиянием изменения факторного признака х. Уравнение (1) показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у, приходящуюся на единицу вариации х. Знак а₁ указывает направление этого изменения.

Параметры уравнения a₀ , a₁ определяют путем решения системы нормальных уравнений, полученной на основе метода наименьших квадратов.

В основу этого метода положено требование минимальности сумм квадратов отклонений фактических данных (у_i ) от выровненных (y_xi ):

S (у_{i -} y_xi ) ² = S (у_{i -} а_{0 -} а₁ ×х_i ) ² ®min, (2)

Так, для уравнения парной линейной зависимости система уравнений имеет следующий вид:

(3)

(4)

Параметры уравнения прямой будут иметь следующий вид:

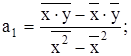(5)

. (6)

Определив значения а₀ , а₁ и подставив их в уравнение связи , находим значение у_х , зависящее только от заданного значения х.

Для прямолинейных зависимостей измерителем тесноты связи между признаками является коэффициент парной корреляции, который рассчитывается по формуле:

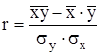, (7)