Учебное пособие: Статистическое изучение взаимосвязи социально-экономических явлений и процессов

; (8)

- среднее значение факторного признака:

; (9)

- среднее значение результативного признака:

; (10)

- среднее квадратическое отклонение результативного признака:

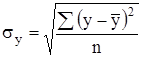; (11)

- среднее квадратическое отклонение факторного признака:

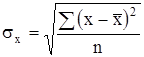. (12)

Квадрат линейного коэффициента корреляции называется линейным коэффициентом детерминации:

r² = d. (13)

Коэффициент детерминации показывает, какая часть общей вариации результативного признака (y) объясняется влиянием изучаемого фактора (x).

Для получения выводов о практической значимости синтезированных в анализе моделей, показаниям тесноты связи дается качественная оценка. Это осуществляется на основе шкалы Чеддока.

Таблица 1 - Шкала Чеддока

Показания тесноты связи	0,1 - 0,3	0,3 - 0,5	0,5 - 0,7	0,7 - 0,9	0,9 - 0,999
Характеристика силы связи	слабая	умеренная	заметная	высокая	весьма высокая

При r = 1 связь является функциональной, при r= 0 связь отсутствует. Если коэффициент корреляции со знаком "+", то связь прямая, если со знаком "-", то связь обратная.

Для практического использования моделей регрессии важна оценка их адекватности, т.е. соответствия фактическим статистическим данным.

Поскольку корреляционно-регрессионный анализ связи между признаками проводится для ограниченной по объему совокупности, то параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенной статистической модели.

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения условий: не являются ли полученные значения параметров результатом действия случайных причин.

Значимость параметров простой линейной регрессии осуществляется с помощью t-критерия Стьюдента. При этом вычисляют фактические (расчетные) значения t-критерия:

для параметра а₀ :

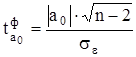, (14)

где - средне квадратическое отклонение результативного признака

у от выровненных значений у_x , которые рассчитываются по уравнению регрессии: