Учебное пособие: Статистическое изучение взаимосвязи социально-экономических явлений и процессов
2.3 Построить на графике поле корреляции и эмпирическую линию корреляционной связи.
2.4 Построить регрессионную модель парной корреляционной зависимости и определить её параметры.
2.5 Построить на графике теоретическую кривую корреляционной зависимости.
2.6 Рассчитать показатели тесноты связи между выработкой рабочего и стажем работы. Дать качественную оценку степени тесноты связи.
2.7 Оценить существенность параметров регрессивной модели и показателей тесноты связи. Дать оценку надёжности уравнения регрессии.
2.8 Дать экспериментальную интерпретацию параметров построенной регрессионной модели.
2.9 На основании регрессионной модели парной зависимости указать доверительные границы, в которых будет находиться прогнозное значение уровня производительности труда рабочего бригады, если стаж его работы составит 10,5 лет при уровне доверительной вероятности 95%.
Решение:
Установим результативный и факторный признаки: результативный признак (y) - выработка, факторный (x) - стаж работы, лет.
Определим наличие и форму корреляционной связи между производительностью труда рабочих бригады и стажем работы. Так как увеличение значений признака-фактора влечёт за собой увеличение величины результативного признака. То можно предположить наличие прямой корреляционной связи между выработкой и стажем работы. Проведём группировку работников бригады по признаку-фактору - стажу работы. Результаты оформим в таблицу 2. Сравнив средние значения результативного признака по группам, можно сделать вывод о наличии связи между выработкой и стажем работы. Причём она будет являться прямой, так как рост значений признака фактора влечёт рост средних значений признака результата.
Построим поле корреляции.
 |
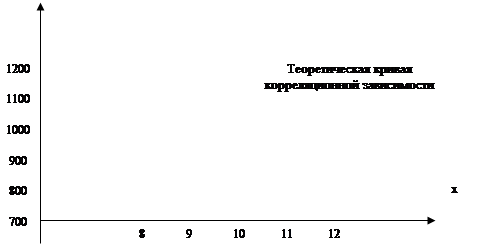??????? 1. ???? ??????????
Построим регрессионную модель парной корреляционной зависимости и определим её параметры: 
- уравнение парной линейной корреляционной зависимости (регрессионная модель).
→
, 
→
Таблица 2 - Расчётная таблица.
 |  |  |  |  |  |  |  |  |  |  |  |
| 8 | 800 | 6400 | 640000 | 64 | 789,02 | -1,95 | 3,8025 | 152,5 | 23256,25 | 10,98 | 120,56 |
| 8 | 850 | 6800 | 722500 | 64 | 102,5 | 10506,25 | 60,98 | 3718,56 | |||
| 8 | 720 | 5760 | 518400 | 64 | 232,5 | 54056,25 | -69,02 | 4763,76 | |||
| 9 | 850 | 1650 | 722500 | 81 | 872,86 | -0,95 | 0,9025 | 102,5 | 10506,25 | -22,86 | 622,57 |
| 9 | 800 | 7200 | 640000 | 81 | -152,5 | 23256,3 | -72,86 | 5308,57 | |||
| 9 | 880 | 7920 | 774400 | 81 | -72,5 | 5256,25 | 7,14 | 50,98 | |||
| 9 | 950 | 8550 | 902500 | 81 | 2,5 | 6,25 | 77,14 | 5950,57 | |||
| 9 | 820 | 7380 | 672400 | 81 | -132,5 | 17556,25 | -52,86 | 2794,17 | |||
| 10 | 900 | 9000 | 810000 | 100 | 956,7 | 0,05 | 0,0025 | -52,5 | 2756,25 | -56,7 | 3114,89 |
| 10 | 1000 | 10000 | 1000000 | 100 | 47,5 | 2256,25 | 43,3 | 1874,89 | |||
| 10 | 920 | 9200 | 846400 | 100 | -32,5 | 1056,25 | -36,7 | 1346,89 | |||
| 10 | 1060 | 10600 | 1123600 | 100 | 107,5 | 11556,25 | 103,3 | 10670,89 | |||
| 10 | 950 | 9500 | 902500 | 100 | 2,5 | 6,25 | -6,7 | 44,89 | |||
| 11 | 900 | 9900 | 810000 | 121 | 1040,54 | 1,05 | 1,1025 | -52,5 | 2756,25 | -140,54 | 975,15 |
| 11 | 1200 | 13200 | 1440000 | 121 | 247,5 | 61256,25 | 159,46 | 25421, 19 | |||
| 11 | 1150 | 12650 | 1322500 | 121 | 197,5 | 39006,5 | 109,46 | 11981,49 | |||
| 11 | 1000 | 11000 | 1000000 | 121 | 47,5 | 2256,25 | -40,54 | 1643,49 | |||
| 12 | 1200 | 14400 | 1440000 | 144 | 1124,38 | 2,05 | 4, 2025 | 247,5 | 6156,25 | 75,62 | 5718,38 |
| 12 | 1100 | 13200 | 1210000 | 144 | 147,5 | 21756,25 | -24,38 | 594,38 | |||
| 12 | 1000 | 12000 | 1000000 | 144 | 47,5 | 2256,25 | -124,38 | 5470,38 | |||
| 199 | 19050 | 192310 | 2013 | 19050,16 | 32,95 | 358275 | 12969,33 |
Найдём среднее произведение факторного и результативного признака по формуле (8):
.
Рассчитаем средние значение факторного и результативного признака:
факторного по формуле (9):
.
результативного, по формуле (10):
; 
.
Подставим значения результативного и факторного признака в уравнение парной линейной корреляционной зависимости получим регрессионную модель парной корреляционной зависимости: 
- регрессионная модель зависимости выработки от стажа работы.
; 
.
5. Построим на графике теоретическую кривую корреляционной зависимости.
6. Рассчитаем показатели тесноты связи между выработкой рабочего и стажем работы. Для прямолинейных зависимостей измерителем тесноты связи между признаками является коэффициент парной корреляции, который рассчитывается по формуле (7).
Для расчёта коэффициента парной корреляции рассчитаем среднее квадратическое отклонение факторного и результативного признака:
результативного признака, по формуле (11)