Учебное пособие: Статистическое изучение взаимосвязи социально-экономических явлений и процессов
для параметра а1 :
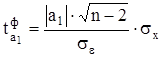 . (16)
. (16)
Вычисленные по формулам (13) и (15) значения, сравниваются с критическими tк , которые принимаются согласно данным таблицы Стьюдента с учетом заданного уровня значимости (a) и числа степеней свободы (k = n- 2). В социально-экономических исследованиях уровень значимости a обычно принимают равным 5%, т.е. a = 0,05, что соответствует доверительной вероятности 95%. Параметр признается существенным при условии, если tф > tк . В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, также могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости линейного коэффициента корреляции r применяется t-критерий Стьюдента. При этом определяется фактическое (расчетное) значение критерия ( tr ф ):
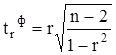 , (17)
, (17)
где n-2 - число степеней свободы при заданном уровне значимости a и объеме выборки n.
Вычисленное значение tr ф сравнивается с критическим tk , которое берется из таблицы Стьюдента с учетом заданного уровня значимости a и числа степеней свободы k = n - 2.
Если tr ф > tk , то это свидетельствует о значимости линейного коэффициента корреляции r и существенности связи между признаком-фактором и признаком-результатом.
Поскольку не все фактические значения результативного признака лежат на линии регрессии, более справедливо для записи уравнения корреляционной зависимости воспользоваться следующей формулой:
![]() , (18)
, (18)
где e - отражает случайную составляющую вариации результативного признака.
В некоторых случаях рассеяние точек корреляционного поля настолько велико, что для принятия решений в управлении не целесообразно пользоваться уравнением регрессии, так как погрешность в оценке анализируемого показателя будет чрезвычайно велика. Для всей совокупности наблюдаемых значений рассчитывается средняя квадратическая ошибка уравнения регрессии, которая представляет собой среднее квадратическое отклонение фактических значений результативного признака у относительно значений, рассчитанных по уравнению регрессии ух :
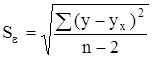 . (19)
. (19)
Среднюю квадратическую ошибку уравнения регрессии Se сравнивают со средним квадратическим отклонением результативного признака sу . Если Se < sу , то использование уравнения регрессии в статистическом анализе является целесообразным.
Таким образом, опираясь на оценку существенности параметров уравнения регрессии и значений линейного коэффициента корреляции, а также на основании оценки надежности уравнения регрессии, дают заключение об адекватности построенной регрессионной модели и возможности распространения выводов, полученных по результатам малой выборки на всю генеральную совокупность.
После проверки адекватности, установления точности и надежности регрессионной модели необходимо ее проанализировать, т.е. дать экономическую интерпретацию параметров регрессии.
Для уравнения парной линейной зависимости прежде всего необходимо проверить согласуется ли знак параметра а1 с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак. Для удобства интерпретации параметра а1 следует использовать коэффициент эластичности:
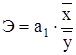 . (20)
. (20)
Коэффициент эластичности показывает среднее изменение результативного признака при изменении факторного признака на 1% и вычисляется в% -ах.
Уравнение регрессионной зависимости является базой для расчета прогнозных значений результативного признака, стоящих за пределами изучаемого ряда. Для осуществления прогноза значений результативного признака по уравнению регрессии используют не дискретные (точечные), а интервальные оценки.
Средняя квадратическая ошибка уравнения регрессии дает возможность в каждом отдельном случае с определенной вероятностью указать, что величина результативного признака расположена в определенном интервале относительно значения, вычисленного по уравнению регрессии.
Зная дисперсию результативного показателя у и задаваясь уровнем доверительной вероятности, определяют доверительные границы прогнозного значения результативного признака упрогноз при значении факторного признака хо по формуле:
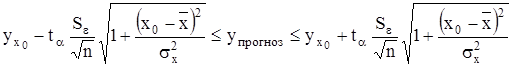 , (21)
, (21)
где ухо - дискретная (точечная) оценка прогнозного значения результативного признака у, рассчитанная по уравнению регрессии, при заданном значении факторного признака хо ;
t a - критерий Стьюдента, который для линейной зависимости определяется в соответствии с уровнем значимости a по распределению Стьюдента с k = n- 2 степенями свободы;
При практическом использовании уравнения регрессии следует помнить, что экстраполяция, т.е. нахождение прогнозируемых уровней за пределами изучаемого ряда, допускается только тогда, когда существенно не изменяются условия формирования уровней признаков, которые лежат в основе определения параметров уравнения регрессии. В противном случае использование уравнений для составления прогнозов должно быть отвергнуто.
2. Пример выполнения лабораторной работы
2.1 Задание на лабораторную работу
На основе ранжированных данных о производительности труда и стаже работы двадцати рабочих бригады (таблица) необходимо:
2.1 Установить результативный и факторный признаки.