Учебное пособие: Теория и технология холодной листовой штамповки

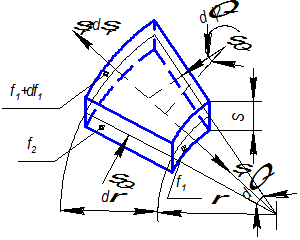
Составим уравнение равновесия на бесконечно малый элемент фланца заготовки.

Составим уравнение равновесия сил, действующих на координату . На две другие координаты смысла составления уравнений нет, так как они обращаться в тождество.

0=0 0=0

Раскрыв скобки уберем величины, которые на порядок меньше остальных, а также учтем, что , тогда получим

,

(1)

Найдем значения площадей:

, (2)

. (3)

Подставив (2) и (3) в (1) получим:

(4)

Уравнение (4) содержит 2 неизвестных и .

Условие пластичности по максимальным касательным напряжениям:

. (5)

определяет схему напряженного состояния, в нашем случае .

,

,

.

Условие пластичности (без учета упрочнения)(5) запишется следующим образом:

(6)

Подставив в (4) уравнение (6), получим дифференциальное уравнение с разделяющимися переменными:

. (7)

Проинтегрировав уравнение (7) получим:

.

Граничные условия: , тогда постоянная интегрирования