Учебное пособие: Вычисление определенного интеграла
Если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем
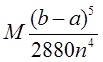
где М - наибольшее значение 
на отрезке [a, b]. Так как n4 растет быстрее, чем n2 , то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций.
Пример
Вычислим интеграл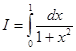 
Этот интеграл легко вычисляется: 
Возьмем n равным 10, h=0.1, рассчитаем значения подынтегральной функции 
в точках разбиения 
, а также полуцелых точках 
.
По формуле средних прямоугольников получим Iпрям =0.785606 (погрешность равна 0.027%), по формуле трапеций Iтрап =0.784981 (погрешность около 0,054. При использовании метода правых и левых прямоугольников погрешность составляет более 3%.
Для сравнения точности приближенных формул вычислим еще раз интеграл
,
но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0 =0, х1 =1/4, х2 =1/2, х3 =3/4, х4 =1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках: у0 =1,0000, у1 =0,8000, у2 =0,6667, у3 =0,5714, у4 =0,5000.
По формуле Симпсона получаем
Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f(4) (x)=24/(1+x)5 , откуда следует, что на отрезке [0, 1] 
. Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 44 )=0.0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.
Сравнение методов по точности
Сравним методы по точности, для этого произведем вычисления интеграла функций y=x, y=x+2, y=x2 , при n=10 и n=60, a=0, b=10. Точное значение интегралов составляет соответственно: 50, 70, 333.(3)
таблица 1
|
метод |
n |
x |
x+2 |
x2 |
|
Метод средних прямоугольников |
10 |
50 |
70 |
332.5 |
|
Метод правых прямоугольников |
10 |
45 |
К-во Просмотров: 409
Бесплатно скачать Учебное пособие: Вычисление определенного интеграла
|