Учебное пособие: Вычисление определенного интеграла
Задача численного интегрирования функций заключается в вычислении приближенного значения определенного интеграла:
, (1)
на основе ряда значений подынтегральной функции .{ f(x) |x=xk = f(xk ) = yk }.
Формулы численного вычисления однократного интеграла называются квадратурными формулами, двойного и более кратного – кубатурными.
Обычный прием построения квадратурных формул состоит в замене подынтегральной функции f(x) на отрезке [a,b] интерполирующей или аппроксимирующей функцией g(x) сравнительно простого вида, например, полиномом, с последующим аналитическим интегрированием. Это приводит к представлению
В пренебрежении остаточным членом R[f] получаем приближенную формулу
.
Обозначим через yi = f(xi ) значение подинтегральной функции в различных точках 
на [a,b]. Квадратурные формулы являются формулами замкнутого типа, если x0 =a , xn =b.
В качестве приближенной функции g(x) рассмотрим интерполяционный полином на 
в форме полинома Лагранжа:
,
где
, при этом 
, где 
- остаточный член интерполяционной формулы Лагранжа.
Формула (1) дает
, (2)
где
. (3)
В формуле (2) величины {
} называются узлами, {
} – весами, 
- погрешностью квадратурной формулы. Если веса {
} квадратурной формулы вычислены по формуле (3), то соответствующую квадратурную формулу называют квадратурной формулой интерполяционного типа.
Подведем итог.
1. Веса {} квадратурной формулы (2) при заданном расположении узлов не зависят от вида подынтегральной функции.
2. В квадратурных формулах интерполяционного типа остаточный член Rn [f] может быть представлен в виде значения конкретного дифференциального оператора на функции f(x). Для 
.
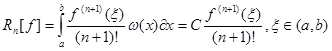3. Для полиномов до порядка n включительно квадратурная формула (2) точна, т.е. 
. Наивысшая степень полинома, для которого квадратурная формула точна, называется степенью квадратурной формулы.
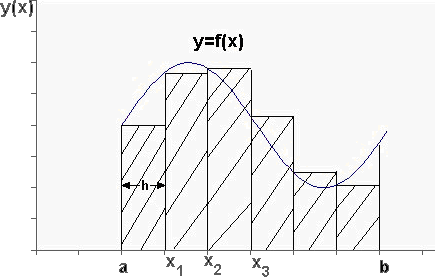
Рассмотрим частные случаи формул (2) и (3): метод прямоугольников, трапеций, парабол (метод Симпсона). Названия этих методов обусловлены геометрической интерпретацией соответствующих формул.
Метод прямоугольников
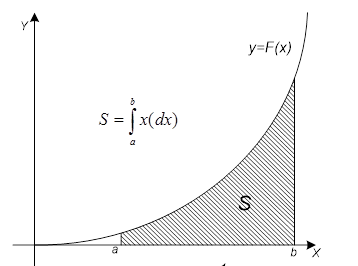
Определенный интеграл функции от функции f(x):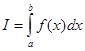 
численно равен площади криволинейной трапеции, ограниченной кривыми у=0, x=a, x=b, y=f(x) (рисунок. 1).
????? ???????? ???? ??????????????? ??????????? ?? ???????
(4)
Метод, представленный формулой (4), называется методом левых прямоугольников, а метод, представленный формулой(5) – методом правых прямоугольников:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--