Дипломная работа: Дослідження сервоприводу з урахуванням нелінійності

Ідея методів витікає з фізичних уявлень про процес встановлення режиму в системі із зворотним зв'язком як ітернаційному процесі поступового багатократного обходу зовнішнього обурення по замкнутому контуру.

При цьому інтегральне рівняння, неявно задаюче перетворення із зворотним зв'язком, може розв'язуватися по схемі

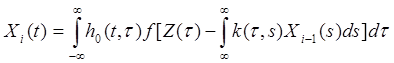(1.2)

причому X₀ (t)=Z(t), тобто значення X(t) передбачається тим, що запізнюється, і кожного разу береться з попереднього ітераційного циклу.

Формально, звичайно, можна розглядати цю схему як звичайну математичнусхему послідовних наближень, не пов'язуючи її з яким-небудь фізичнимзмістом.

Очевидно. що вживання цієї схеми зводить задачу про замкнуту систему до задачі про розімкнену.

Наближені методи, засновані на припущенні про те, що характерзакону розподілу сигналу на вході нелінійного безінерційного перетвореннявідомий.

В цьому випадку розшукується лише деяка кількість числових параметрів, залишених невизначеними в рівнянні закону розподілу. Для цих параметрів виходять неявні співвідношення (звичайно трацендентнірівняння), які можуть бути дозволені, наприклад, графічно. Маючи у вигляді, що при фільтраціївідбувається наближення закону розподілу до нормального, звичайно приймаютьсаме такий характер закону. Нормальний закон повністю визначаєтьсявеличинами середнього m_X і середньоквадратичного σ_X значення, а також видом кореляційноїфункції.

В основному методі цієї групи додатково використовується можливість статичної лінеаризації безінерційного нелінійного перетворення, а отже, вводиться припущення про те, що можна у виразі для кореляційної функції сигналу X(t) на вході. Це дозволяє істотно спростити задачу і оперувати тільки параметрами m_X і σ_X .

Використовування ідеї розкладання по малому параметру дозволяє розширити можливості методу і враховувати малі спотворення виду кореляційної функції і відхилення закону розподілу від номінального.

Зважаючи на спільність і порівняльну простоту метод статичної лінеаризації представляє найбільший інтерес для розрахункової практики.

Виклад проблем, пов'язаних з дослідженням нелінійних перетворень із зворотним зв'язком, доцільно розділити на дві частини: першу, присвячену дослідженню стаціонарних режимів, тобто режимів, при яких сигнал, діючий всередині контуру зворотного зв'язку, є стаціонарною функцією часу, і другу, де розглядаються нестаціонарні режими [3].

Від режиму, який реалізується в даній системі (перетворення), визначається не її структурою, а характеристиками вхідних сигналів і значеннями параметрів системи.

При дослідженні конкретних систем звичайно доводиться аналізувати і стаціонарні, і нестаціонарні режими.

Вельми важливими практичним питанням є з'ясування умов переходу від одного режиму до іншого при зміні параметрів сигналу системи.

Ці умови у ряді випадків визначають так звану перешкодостійкість системи, тобто можливість втрати стійкості через наявність випадкових перешкод.

Методи дослідження і розрахунку нелінійних стежачихсистем, що розглядаються нижче, базуються на гармонійній лінеаризації динамічнихвластивостей нелінійних елементів [9].

Досліджуваний елекрогідропривод розглядатимемо за допомогою методу гармонійноїлінеаризації динамічних властивостей нелінійних елементів.

Метод гармонійної лінеаризації заснований на заміні нелінійного елементаеквівалентним (по деяких властивостях) лінійним. Умовою еквівалентностіслужить збіг вихідних коливань лінійної ланкиз першою гармонікоювихідних коливань нелінійного, коли на їх вхід подається однаковийгармонійний сигнал x=Asinωt.

Якщо характеристика нелінійного елемента однозначна і симетричнащодо початку координат, то еквівалентний лінійний елемент може описуватися рівняннямy=q(А) x.

де х – вхідна координата; у – вихідна координата; q(А) – коэффициентгармонійноїлінеаризації.

У разі неоднозначних (петлевих) нелінейностей перша гармоніка вихідногосигналу зсунута по фазі щодо вхідного сигналу: цією ж здатністювинен володіти й эквівалентний лінійний елемент, томупри лінеаризації використовується лінійний елемент, властивості якого визначаютьсярівнянням

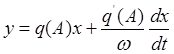. (1.3)

Передавальна функція в даному випадку виражається

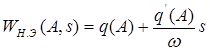, (1.4)

частотна характеристика (s=jω):

. (1.5)

Вибір коефіцієнтів і повинен забезпечити рівність між вихіднимиколиваннями еквівалентного лінійного і першою гармонікою реальногонелінійного елемента.

В ще більш загальному випадку коефіцієнти гармонійної лінеаризації можуть залежати і від частоти:, а частотна характеристика нелінійного елемента прийме вигляд: