Дипломная работа: Инверсия плоскости в комплексно сопряженных координатах

· доказательство ряда теорем при помощи инверсии комплексной плоскости.

Оказалось, что не так много специальных работ по теме. Инверсия комплексной плоскости оказалась крайне слабо освещена в литературе по сравнению с инверсией евклидовой плоскости. Поступали следующим образом: брали известный факт из евклидовой плоскости, а потом доказывали его методом комплексно сопряженных координат. Чаще всего такие доказательства были понятнее и короче, чем исходные.

Глава 1

Основные положения теории инверсии

1.1. Общие сведения о комплексной плоскости . Зададим на плоскости прямоугольную декартову систему координат 0xy . Тогда каждому комплексному числу z , представленному в алгебраической форме , можно однозначно поставить в соответствие точку М плоскости с координатами . Комплексное число z называют комплексной координатой соответствующей точки М и пишут: .

Следовательно, множество точек евклидовой плоскости находится во взаимно однозначном соответствии с множеством комплексных чисел. Эту плоскость называют плоскостью комплексных чисел.

Все необходимые сведения об этой плоскости очень хорошо даны в книге Я. П. Понарина [3]. Здесь приведем лишь некоторые формулы, взятые из того же источника, использованные в работе.

Расстояние между двумя точками с координатами а и b равно .

Уравнение прямой в канонической форме: , .

Уравнение окружности с центром в точке s и радиусом r : . Также часто используют запись , , , где центр , радиус .

Скалярное произведение векторов: .

Коллинеарность трех точек с координатами а , b и с : .

Критерий коллинеарности векторов: .

Расстояние от точки с координатой z ₀ до прямой , : .

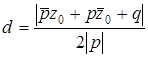Критерий параллельности двух прямых и , заданных в канонической форме: .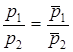

Критерий перпендикулярности двух прямых и , заданных в канонической форме: .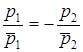

Двойное отношение четырех точек плоскости с координатами а , b , с иd : ; аргумент w равен ориентированному углу между окружностями abc и abd .

Критерий принадлежности четырех точек одной окружности или прямой: .

Критерий ортогональности окружностей , и , : .

Параллельный перенос на вектор с координатой r : .

Гомотетия с центром s и коэффициентом s : , .

Осевая симметрия с осью симметрии , где : .

Центральная симметрия с центром : .

1.2. Определение инверсии – симметрии относительно окружности . [1]

Определение 1 . Углом между двумя окружностями называется угол между касательными к окружностям в точке их пересечения.

Если окружности не имеют общих точек, то угол между ними не определен.

Определение 2. Углом между окружностью S и прямой l называется угол между прямой l и касательной к окружности S в точке пересечения этой окружности с l .

Опять же, если прямая и окружность не имеют общих точек, то угол между ними не определен.

Из определения 2 следует, что окружности, центры которых лежат на данной прямой l , и только эти окружности, перпендикулярны к прямой l .

Теорема 1 . Все окружности, перпендикулярные прямой l и проходящие через точку А , проходят и через точку В , симметричную точке А относительно прямой l .

□ Рассмотрим произвольную окружность с центром на прямой l , проходящую через точку А . Введем систему координат таким образом, что прямая l является действительной осью, а начало координат располагается в центре нашей окружности, и радиус ее равен 1.