Дипломная работа: Инверсия плоскости в комплексно сопряженных координатах

5Þ4. Проведем окружность с центром в точке S и радиусом . Нам дано, что . Но любая окружность, перпендикулярная проведенной и проходящая через точку М , не лежащую на проведенной окружности, проходит и через точку М ’, мы это показали ранее. Значит, действительно, точки М и М ’ симметричны в смысле определения 4.

Чтобы это было действительно преобразование, допускают, что точка S отображается в бесконечно удаленную точку, и наоборот (в данном случае нам удобнее мыслить бесконечно удаленную область как одну точку).

Определение 5 менее геометрично, чем предыдущее, но обладает преимуществом большей простоты. Исходя из этого определения, инверсию иногда еще называют преобразованием обратных радиусов. С этим определением связано также название «инверсия» (от латинского слова inversio – обращение).

Очевидно, слова «точка М ’ лежит на луче SM и произведение » можно с успехом заменить словами «точки S , M и М ’ коллинеарны и скалярное произведение векторов ». Здесь k всегда положительно. Но иногда полезно рассмотреть преобразование, которое переводит точку M в М ’ так, что и точки S , M и М ’ коллинеарны, но M и М ’ лежат по разные стороны от точки S . Тогда, очевидно, k будет отрицательным. Такое преобразование называют инверсией с центром в точке S и отрицательной степенью. Здесь также допускают, что центр инверсии переходит в бесконечно удаленную область, и наоборот.

Вообще, говоря об инверсии, имеют в виду обычно инверсию с положительной степенью. Если знак степени инверсии может быть любым, то такое преобразование называют обобщенной инверсией. Его определение будет таким.

Определение 6 . Обобщенной инверсией плоскости с центром в точке S и степенью инверсии k называется преобразование, которое всякую точку М плоскости, отличную от S , отображает в такую точку М ’, что точки S , M и М ’ коллинеарны и скалярное произведение векторов . При этом считают, что S переходит в бесконечно удаленную область, и наоборот.

Это преобразование инволютивное, поскольку точки М и М ’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно.

1.3. Формула инверсии в комплексно сопряженных координатах . Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S , M и М ’ соответствуют комплексные числа s , z и z ’.

По формуле скалярного произведения векторов . Коллинеарность точек S , M и М ’ дает равенство . Отсюда имеем Û, откуда и получаем искомую формулу .

Итак, обобщенная инверсия имеет формулу или, что то же самое, . При k >0 получаем инверсию с положительной степенью, при k <0 – с отрицательной.

Но всякое ли преобразование плоскости, заданное формулой , является обобщенной инверсией? Если принять , , то достаточно потребовать, чтобы и для обобщенной и для обычной инверсии (с положительной степенью).

Значит, всякое преобразование плоскости, задаваемой формулой , есть обобщенная инверсия.

1.4. Неподвижные точки и окружность инверсии. Исследуем уравнение инверсии на неподвижные точки: для них должно выполняться равенство Û. Мы не рассматриваем центр инверсии и бесконечно удаленную область, так как мы доопределили, что они не остаются неподвижными, а переходят друг в друга. Тогда будет выполняться равенство .

Очевидно, что если , то все искомые точки образуют окружность с центром в точке с координатой s и радиусом . Эта окружность при называется окружностью инверсии. Если обозначить радиус окружности инверсии через R , то выполняется . И формулу инверсии для k >0 можно переписать более наглядно: .

Если степень инверсии отрицательна, то преобразование не имеет неподвижных точек (поскольку невозможно изобразить на плоскости, даже комплексной, точки, координаты которых удовлетворяют равенству ). Но иногда эту мнимую окружность также называют окружностью инверсии, ее центр расположен в центре инверсии, а радиус будет равен ==.

Так как , то, очевидно, инверсию отрицательной степени легко представить в виде коммутативной композиции инверсии с положительной степенью и центральной симметрии с общим центром в s .

1.5. Образы прямых и окружностей при обобщенной инверсии. Без ограничения общности рассуждений можно принять , и формула инверсии примет вид , более удобный для практики. Ведь нам пока не важны коэффициенты в получающейся формуле, важно, какую фигуру она описывает.

Пусть задана прямая l с уравнением , . При подстановке в это уравнение и получаем: . Умножим на , это будет равносильным преобразованием, поскольку ; получим, опуская в полученном результате штрихи: .

Если q = 0, то получаем уравнение . Так как , то умножим обе части уравнения на , получим . Это уравнение прямой, совпадающей с заданной прямой l . Если , то получаем уравнение окружности , так как 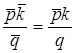. Она содержит центр инверсии, ее центр расположен в точке , а радиус равен . Заметим, что центр лежит на прямой , проходящей через центр инверсии перпендикулярно l .

Итак, прямая, содержащая центр инверсии, отображается при этой инверсии в себя; прямая, не содержащая центр инверсии, отображается в окружность, проходящую через него. Поскольку инверсия инволютивна, то окружность, содержащая центр инверсии, отображается в прямую, не содержащую его.

Возьмем теперь окружность , не проходящую через центр инверсии . Тогда выполняется . Ее образ имеет уравнение (штрихи опущены). При раскрытии скобок получим . Умножим на , это будет равносильным преобразованием, поскольку ; получим . Так как , то этим уравнением задается окружность с центром и радиусом 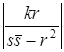. Она не проходит через центр инверсии. Интересно, что центр инверсии 0 , центр данной окружности s и центр ее образа коллинеарны, поскольку число действительное. Но центр окружности при инверсии не переходит в центр окружности образа. Если центр данной окружности s перейдет в , то тогда должно выполняться . Поскольку , умножим на , получим равносильное равенство . Отсюда , то есть , что невозможно. Значит, предположение было неверно, и центр данной окружности не переходит в центр окружности образа.

Итак, окружность, не проходящая через центр инверсии, переходит в окружность, также не проходящую через центр инверсии.

В частности, если центр инверсии совпадает с центром окружности, то и окружность при инверсии переходит в окружность 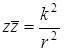, центр которой также совпадает с центром инверсии. Итак, окружность, центр которой совпадает с центром инверсии, при этой инверсии переходит в концентрическую окружность. В частности, окружность с уравнением инвариантна.

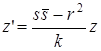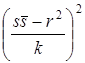Интересно, что центр инверсии является одновременно и центром гомотетии, переводящей одну окружность в другую. Для нашего случая гомотетия будет иметь уравнение . Убедиться в этом можно простой подстановкой: эта гомотетия переводит окружность в фигуру . Поделив обе части на , получим окружность с центром и радиусом 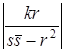, что и требовалось доказать.

Теперь становится ясно, что каждую окружность можно при помощи подходяще выбранной инверсии перевести в другую данную окружность или прямую. Докажем это.

Пусть даны две окружности действительного радиуса. Рассмотрим сначала случай, когда их радиусы не равны.

Мы уже показали, что центры окружностей и центр инверсии должны лежать на одной прямой. Понятно, что центр инверсии не лежит на данных окружностях.

Точки, лежащие на прямой центров, переходят в точки, лежащие на той же прямой. Поэтому могут быть два порядка точек: и .

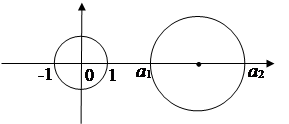Введем систему координат таким образом, что центры окружностей лежат на действительной оси, причем центр одной совпадает с началом координат, а радиус ее равен 1.