Дипломная работа: Инверсия плоскости в комплексно сопряженных координатах

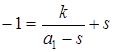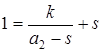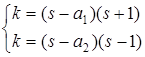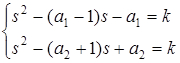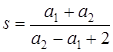Пусть точки пересечения второй окружности с действительной осью имеют координаты а ₁ и а ₂ . Тогда при инверсии а ₁ переходит в -1, а а ₂ – в 1. Тогда можно записать, что , . То есть получаем систему: , что равносильно . Вычтем: , откуда, в силу неравности радиусов, . Может статься, что это не является решением. Решением это будет в точности тогда, если совпадут значения k из обоих уравнений.

Из первого уравнения = .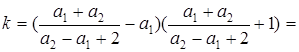

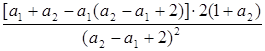Из второго условия получаем =. Тот же самый результат. Итак, получаем единственную инверсию с центром в точке 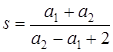и степенью .

Точка с координатой а ₂ лежит на действительной оси правее точки с координатой а ₁ , поэтому для определения знака степени нужно знать знак произведения .

Степень инверсии будет положительна в двух случаях: либо , откуда , либо , откуда , то есть когда одна окружность лежит целиком внутри другой. В остальных случаях степень инверсии будет отрицательна.

Рассмотрим второй случай. Тогда при инверсии а ₁ переходит в 1, а а ₂ – в -1. Можно записать, что , . То есть получаем систему: , что равносильно . Вычтем: , откуда, в силу неравности радиусов, .

Аналогично, может оказаться, что это не является решением. Решением это будет в точности тогда, если совпадут значения k из обоих уравнений.

Из первого уравнения , откуда . Из второго уравнения = . Тот же самый результат.

Знак степени определяется знаком произведения . Отрицательна она будет только в случае , то есть или в случае , то есть . Это происходит в точности когда одна окружность лежит внутри другой. Положительной степень будет в противном случае.

Итак, когда радиусы окружностей не равны, одну в другую можно перевести ровно двумя инверсиями, причем одна из них с положительной степенью, а другая – с отрицательной.

Если же радиусы окружностей равны, то все выкладки будут иметь место, но гораздо упростятся. Для первого случая получим из равенства 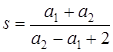, что , тогда . Причем у нас не может быть случая, когда одна окружность лежит внутри другой, значит, степень положительна.

Для второго же случая получаем верное равенство , но , и получим , то есть окружности концентричны, но в силу равенства радиусов они совпадают. Это невозможно по предположению, значит, такой инверсии не может быть.

Можно сделать вывод, что если радиусы окружностей равны, то одну в другую можно перевести ровно одной инверсией с положительной степенью. В принципе, этого следовало ожидать: у двух окружностей равного радиуса только один центр гомотетии.

Покажем теперь, что существует инверсия, переводящая прямую l в окружность действительного радиуса, и обратно. Ясно, что эта окружность проходит через центр инверсии, а прямая нет. Мы уже показали, что центр инверсии лежит на прямой m , проходящей через центр нашей окружности перпендикулярно l . Значит, он может быть только в одной из точек пересечения окружности с прямой m .

Введем систему координат так, что начало координат располагается в центре окружности, а прямая m совпадает с действительной осью.

Данная прямая l параллельна мнимой оси, поэтому будет иметь уравнение , . Прямая пересекает действительную ось в точке с координатой . Окружность, если обозначить ее радиус r , будет иметь уравнение . Инверсии, если они есть, будут иметь формулы и , где k ₁ и k ₂ нам пока не известны. Первая переведет окружность в прямую с уравнением ÛÛ. Чтобы это была l , достаточно потребовать , откуда .

Вторая инверсия переведет окружность в прямую с уравнением ÛÛ. Чтобы это была l , достаточно потребовать , откуда .

Могут получиться следующие случаи:

1) Û, тогда , ;

2) Û, тогда , , то есть второй инверсии не существует – это происходит при касании прямой и окружности в точке с координатой -r ;

3) Û, тогда , ;

4) Û, тогда , то есть первой инверсии не существует – это происходит при касании прямой и окружности в точке с координатой r , ;

5) Û, тогда , .

Можно сделать вывод, что если прямая не имеет общих точек с окружностью, то одну в другую можно перевести ровно двумя инверсиями, причем одна из них с положительной степенью, а другая с отрицательной. Если прямая касается окружности, то одну в другую можно перевести только одной инверсией с положительной степенью. Если пря?