Дипломная работа: Избранные теоремы геометрии тетраэдра

Доказательство.

Сначала докажем необходимость. Пусть точки А₁ ,В₁ ,С₁ лежат на прямой l и AA₀ =h₁ , CC₀ =h₃ - перпендикуляры, опущенные соответственно из точек А, В, С на прямую l . Из подобия треугольников АА₀ С₁ и ВВ₀ С₁ получаем

. Аналогично, рассматривая другие пары подобных треугольников, получаем ; . Перемножая полученные пропорции, приходим к требуемому равенству.

Теперь докажем достаточность. Пусть точки А₁ , В₁ , С₁ , лежащие на прямых ВС, АС, АВ таковы, что . Докажем, что точки А₁ , В₁ , С₁ лежат на одной прямой.

Проведем прямую А₁ В₁ и докажем, что точка С₁ ей принадлежит. Предположим, что это не так. Сначала заметим, прямая А₁ В₁ не параллельна прямой АВ . Пусть Т - точка пересечения А₁ В₁ и АВ , тогда

. Из условия и равенства (1) следует, что . Так как точки Т и С₁ лежат вне отрезка АВ , их совпадение вытекает из следующей леммы.

Лемма 1.

Пусть А и В две различные точки, тогда для любого k>0, k≠1 на прямой АВ существуют две точки U и V такие, что , причем одна из этих точек принадлежит отрезку АВ, а другая лежит вне отрезка.

Доказательство.

Введем на прямой АВ координаты, приняв точку А за начало координат. Пусть для определенности k> 1, тогда координата искомой точки U , лежащей внутри отрезка АВ , удовлетворяет уравнению , откуда .Точка V находится вне отрезка AB , из уравнения , откуда .Случай 0<k< 1 отличается от рассмотренного лишь тем, что точку V следует искать левее точки А .

Теорема Менелая допускает интересное стереометрическое обобщение.

Теорема Менелая для тетраэдра.

Если плоскость μ пересекает ребра АВ, ВС, CD и DA тетраэдра АВСD в точках А₁ , В₁ , С₁ , D₁ , то (2).

Обратно, если для четырех точек А₁ , В₁ , С₁ , D₁ ,лежащих соответственно на ребрах АВ, ВС, СD, DA тетраэдра, выполнено равенство (2), то эти четыре точки лежат в одной плоскости.

Доказательство.

Пусть h₁ , h₂ , h_3, h₄ - расстояния от точек А, В, С, D соответственно до плоскости μ , тогда ; ; ; .

Осталось перемножить полученные отношения.

Для доказательства обратной теоремы построим плоскость А₁ , В₁ , С₁ . Пусть эта плоскость пересекает ребро DA в точке Т.

По доказанному , а по условию , поэтому (и по лемме) точки Т и D₁ совпадают.Утверждение доказано.

§2. Теорема Чевы

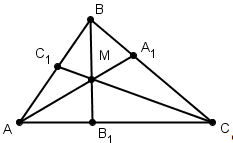
Теорема Чевы для треугольника.

Пусть точки А₁ , В₁ ,С₁ лежат соответственно на сторонах ВС, АС и ВА треугольника АВС (см. рис). Для того чтобы отрезки АА₁ , ВВ₁ , СС₁ пересекались в одной точке, необходимо и достаточно, чтобы выполнялось соотношение: (3) (отрезки АА₁ , ВВ₁ , СС₁ иногда называют чевианами).

Доказательство.

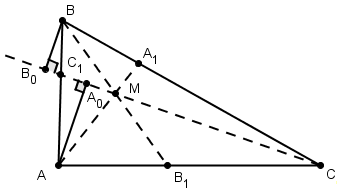
Необходимость. Пусть отрезки АА₁ , ВВ₁ , СС₁ пересекаются в точке М внутри треугольника АВС .