Дипломная работа: Избранные теоремы геометрии тетраэдра

.

С другой стороны

(:

1= ) => .

§2. Ортоцентрические тетраэдры

В отличие от треугольника, высоты которого всегда пересекаются в одной точке - ортоцентре, не всякий тетраэдр обладает аналогичным свойством. Тетраэдр, высоты которого пересекаются в одной точке, называется ортоцентрическим. мы начнем изучение ортоцентрических тетраэдров с необходимых и достаточных условий ортоцентричности, каждое из которых можно принять за определение ортоцентрического тетраэдра.

(1) Высоты тетраэдра пересекаются в одной точке.

(2) Основания высот тетраэдра являются ортоцентрами граней.

(3) Каждые два противоположных ребра тетраэдра перпендикулярны.

(4) Суммы квадратов противоположных ребер тетраэдра равны.

(5) Отрезки, соединяющие середины противоположных ребер тетраэдра, равны.

(6) Произведения косинусов противоположных двугранных углов равны.

(7) Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных ребер.

Докажем некоторые из них.

Доказательство (3).

Пусть каждые два противоположных ребра тетраэдра перпендикулярны.

Следовательно, высоты тетраэдра попарно пересекаются. Если несколько прямых попарно пересекаются, то они лежат в одной плоскости или проходят через одну точку. В одной плоскости высоты тетраэдра лежать не могут, так как иначе в одной плоскости лежали бы и его вершины, поэтому они пересекаются в одной точке.

Вообще говоря, для того чтобы высоты тетраэдра пересекались в одной точке, необходимо и достаточно потребовать перпендикулярность только двух пар противоположных ребер. Доказательство этого предложения напрямую следует из следующей задачи.

Задача 1.

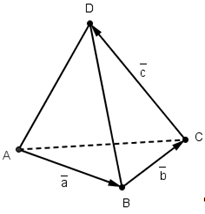
Дан произвольный тетраэдр ABCD . Докажите, что .

Решение.

Пусть а= , b= , с= . Тогда , и , складывая эти равенства, получаем требуемое.

Далее докажем свойство (4).

Пусть а= , b= и с= . Равенство² + ² = ² + ² , что, т.е. (а,с)=0 . Применяя данный алгоритм к другим парам противоположных ребер, очевидно, получим искомое утверждение.

Приведем оказательство свойства (6).

Для доказательства используем следующие теоремы:

- Теорема синусов. «Произведение длин двух противоположных ребер тетраэдра, деленное на произведение синусов двугранных углов при этих ребрах, одно и то же для всех трех пар противоположных ребер тетраэдра».

- Теорема Бертшнейдера. «Если a и b – длины двух скрещивающихся ребер тетраэдра, а - двугранные углы при этих ребрах, то величина не зависит от выбора пары скрещивающихся ребер.