Дипломная работа: Кратные интегралы

где (x₀ , y₀ , z₀ ) – точка из области D, aC – произвольная постоянная.

2.2 Поверхностные интегралы

Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S₁ , S₂ ,…, S_п (при этом площадь каждой части тоже обозначим S_п ). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части S_i точку

M_i (x_i , y_i , z_i ) и составим интегральную сумму

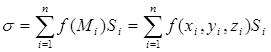
Если существует конечный предел при этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек M_i , то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается

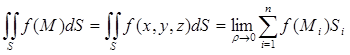. (32)

Если поверхность S задается явным образом, то есть уравнением вида z = φ(x, y), вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла:

(33)

где Ω – проекция поверхности S на плоскость Оху.

Разобьем поверхность Sна части S₁ , S₂ ,…, S_п , выберем в каждой части S_i точку M_i (x_i , y_i , z_i ), и умножим f(M_i ) на площадь D_i проекции части S_i на плоскость Оху. Если существует конечный предел суммы

,

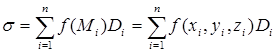не зависящий от способа разбиения поверхности и выбора точек на ней, то он называется поверхностным интегралом второго рода от функции f(M) по выбранной стороне поверхности S и обозначается

(34)

Подобным образом можно проектировать части поверхности на координатные плоскости Оxzи Оyz. Получим два других поверхностных интеграла 2-го рода:

и .

Рассмотрев сумму таких интегралов по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:

(35)

Если D, D΄ и D΄΄ - проекции поверхности S на координатные плоскости Оху, Oxz и Oyz, то

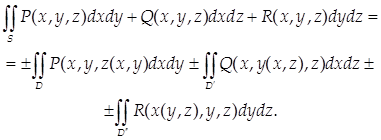(36)

Связь между тройным интегралом по трехмерной области V и поверхностным интегралом 2-го рода по замкнутой поверхности S, ограничивающей тело V, задается формулой Гаусса-Остроградского:

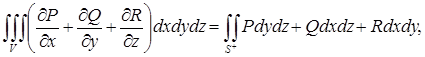(37)

где запись «S⁺ » означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.

Формула Стокса устанавливает связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориентации поверхности:

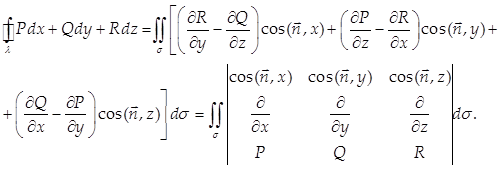(38)

2.3 Геометрические и физические приложения

1) Длина кривой.

Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

(39)