Дипломная работа: Методические особенности изучения темы "Подобные треугольники" в средней общеобразовательной школе

Преобразование подобия плоскости изменяет расстояние между любыми двумя точками плоскости в одном и том же отношении, равном коэффициенту подобия k, т. е. для любых точек М, N и их образов М', N' выполняется равенство |M ^/ N ^/ |=k.

Доказательство. Пусть относительно Oij точки М и N имеют координаты: М(x₁ , y₁ ), N(x₂ , y₂ ). Тогда =

Образы М' и N' точек М, N имеют соответственно те же координаты (x₁ , y₁ ), (x₂ , y₂ ) относительно системы координатO ^/ i ^/ j ^/ . Найдём:

= =====, так как и .

Свойства преобразования подобия.

Преобразование подобия плоскости всякую прямую отображает в прямую.

Преобразование подобия плоскости отображает полуплоскость с границей в полуплоскость с границей где .

Преобразование подобия плоскости сохраняет простое отношение трёх точек прямой.

Преобразование подобия плоскости сохраняет отношение “лежать между”.

Преобразование подобия плоскости отображает угол в равный ему угол.

Преобразование подобия плоскости отображает отрезок в отрезок, луч в луч.

Преобразование подобия плоскости отображает параллельные прямые в параллельные прямые.

Следствие. Преобразование подобия плоскости отображает параллелограмм в параллелограмм.

Преобразование подобия плоскости отображает вектор в вектор, сумму векторов в сумму векторов и произведение числа на вектор в произведение того же числа на соответствующий вектор.

Теорема. Если преобразование подобия f с коэффициентом подобия k задано двумя системами координат Oij иO ^/ i ^/ j ^/ , при этом и O ^/ ( x ₀ , y ₀ ) , то координаты любой точки M ( x , y ) _Oij и её образа M ^/ ( x ^/ , y ^/ ) _O ^/ _i ^/ _j ^/ связанысоотношениями:

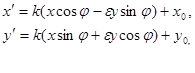где (1)

Доказательство опирается на определение преобразования подобия, на формулы, связывающие координаты одной и той же точки относительно двух прямоугольных декартовых систем координат, на разложение вектора по базисам.

Замечание. При системы координат Oij и O ^/ i ^/ j ^/ одинаково ориентированы, а при противоположено ориентированы.

Определение. Преобразование подобия плоскости, определяемое формулами (1) называется преобразованием подобия первого рода при и преобразованием подобия второго рода при .

Из основного свойства преобразования подобия и верного утверждения, обратного ему (если преобразование плоскости изменяет расстояние между точками в одном и том же отношении, равном k>0, то оно является преобразованием подобия с коэффициентом подобия k), следует другое определение преобразования подобия. Определение. Преобразованием подобия плоскости с коэффициентом подобия k>0 называется преобразование плоскости, изменяющее расстояние между любыми точками в одном и том же отношении, равном k.

Гомотетия плоскости.

Определение. Гомотетией плоскости с центром гомотетии О и коэффициентом гомотетии называется преобразованием плоскости, которое всякой точке М плоскости ставит в соответствии точку М^/ по закону

.

Обозначение. - гомотетия плоскости с центром гомотетии О и коэффициентом гомотетии k.

Определение. Гомотетичными называются фигуры и =.

1) Гомотетичные точки М и М ^/ лежат на одной прямой с центром гомотетии О .

2) Точки М и М ^/ лежат по одну сторону от центра О , если k>0, и – по разные стороны, если k<0.

3) М ^/ N^/ = | k|MN .

4) Гомотетия плоскости является при: